English

• Hydrogen production from solar water splitting, which offers a promising technology to solve the global challenge of the depletion of fossil fuels and the associated environmental pollution, has attracted significant interest over the past years [1-4]. Since the pioneering work of Fujishima and Honda in 1972 [5], numerous inorganic semiconductor materials, including metal oxides, metal sulfides, metal nitrides, and metal phosphides, have been explored for water photolysis [6-12]. Unfortunately, most reported inorganic photocatalysts exhibit intrinsic disadvantages such as wide band gap (>3.0 eV), ineffective utilization of solar energy (can only absorb ultraviolet light), and high electron-hole recombination rate induced by the low carrier mobility and long migration distance [13, 14]. Hence, their photocatalytic performances are still yet to achieve the requirement of practical application.

  Compared to the bulk photocatalysts, two-dimensional (2D) photocatalysts possess unique atomic structures and unprecedented properties, thus have been hot topics of extensive experimental and theoretical researches [15-22]. For instance, Sun et al. [23] reported that the photocurrent density of single-layer SnS₂ reached up to 2.75 mA/ cm² at 1.0 V, which was 72 times larger than the bulk counterpart. Cheng et al. [24] found that the hydrogen generation rates of synthesized FePS₃ sheets were 3 times higher than that of bulk FePS₃. Qiao et al. [25] theoretically predicted that PdSeO₃ monolayer can be easily exfoliated from the bulk phase, and its reduction/oxidation ability was high enough for splitting pure water into hydrogen and oxygen. Most recently, Yang's group designed a new 2D photocatalyst (F-BNBN-H) with large intrinsic dipole, in which the band gap restriction (1.23 eV) for direct overall water splitting can be broken and thus utilizing the near-infrared light would be achieved [26]. Referring to this novel model, some 2D materials with intrinsic electric polarization, such as Janus transition metal dichalcogenides monolayers [27-30], Sc₂CO₂ [31], M₂XY (M=Ga, In; X/Y = S, Se, Te) [32-34] and M₂X₃ (M = Al, Ga, In; X = S, Se, Te) [35, 36], have been exploited as photocatalyts for water splitting. In virtue of the intrinsic electric field produced by the intrinsic dipole, these 2D materials have not only appropriate band gap and band edge alignments, but also very low recombination possibility of photongenerated carriers, making them be promising candidates as highly efficient photocatalysts. Nevertheless, the amount of such built-in dipoled 2D photocatalysts is still rather rare. It is still necessary to search for other 2D semiconductor materials with good structure stability, appropriate electronic properties, and large intrinsic dipoles simultaneously.

  As allotropes of phosphorene, layered group-IV monochalcogenides have been theoretically predicted and experimentally synthesized recently, which show good promise for various applications in these aspects of gas sensors, solar cells, anode materials for ion batteries, and photocatalysts [37-40]. In particular, the monolayer materials in the buckled configuration, similar to blue phosphorene, usually generate the intrinsic dipoles due to by the large difference of electronegativity between the top and bottom sides. Monolayer silicon and germanium monochalcogenides (i.e., SiS, SiSe, GeS and GeSe) have been found to be suitable for overall photocatalytic water splitting [41-44]. Inspired by these, we thus wonder whether the monolayer carbon monochalcogenides (CX, X = S, Se) can steadily exist as free-standing sheets and whether they are high efficient photocatalysts for water splitting. Hence, we systematically investigate the structural, electronic, and photocatalytic properties of blue-phase CX (X = S, Se) monolayers by performing first-principles calculations.

  First-principles calculations are carried out based on the density functional theory with the projector augmented wave method [45], as implemented in Vienna Ab initio Simulation Package (VASP) [46]. The Perdew-Burke-Ernzerhof (PBE) functional [47] is adopted for optimizing the geometric structure, and the Heyd-Scuseria-Ernzerhof (HSE06) functional [48, 49] is adopted for giving more accurate electronic and optical properties, in which the 25% PBE exchange part is replaced by the Hartree-Fock exact exchange in the short-range. Namely, the mixing parameter (α) of the HSE06 functional is set to be 0.25. The energy cutoff energy is set to 500 eV, and the Monkhorst-Pack mesh [50] of k-points 21 × 21 × 1 points are used to sample the Brillouin zone. A vacuum region of 20.0 Å along the z direction is applied to avoid the coupling effect of two adjacent image layers. The convergence criterias of total energy and atomic forces are set as 1 × 10⁻⁵ eV and 0.02 eV/Å, respectively. Dipole correction along the z direction is needed to cancel the errors of electrostatic potential, atomic force, and total energy, caused by periodic boundary condition.

  Akin to blue phosphorene, the CX monolayers have a buckled hexagonal structure with the C and S(Se) atoms interlocked and distributed alternately, as shown in Fig. 1a. After optimization, the lattice constant of monolayer CS is predicted to be 2.82 Å with a C–S bond length of 1.87 Å and buckling height of 0.92 Å, while for monolayer CSe, the lattice parameter, C–Se bond length and buckling height increase to 3.07 Å, 2.06 Å and 1.04 Å, respectively. The reason is that the atomic radius of Se atom is larger than that of S atom. To characterize the bonding features in these CX monolayers, the electron localization functions (ELF) are calculated and depicted in Fig. 1b and Fig. S1 (Supporting information), where the values of 1.0, 0.5 and 0.0 represent the fully localized electron, the free electron-gas and very low electron density, respectively. It can be seen that the ELF values around the C and S(Se) sites are different, and a substantial concentration of electrons are localized at the regions between C and S(Se) atoms, revealing the presence of polar covalent bonding in monolayer CS and CSe. The Bader charge analysis further illustrates that 0.23(0.39) electrons are transferred from S(Se) atom to C atom, also confirming the polar chemical bonding.

  Figure 1

  

  Figure 1.  (a) Geometric structure of CX monolayers from thetop and side views. The hexagonal primitive cell and orthogonal supercell are marked by black and blue lines, respectively. (b) Visualization of the electron localization function for monolayer CS. Calculated phonon dispersions of monolayer (c) CS and (d) CSe. The total energy fluctuations during 10 ps AIMD simulations at room temperature (300 K) for monolayer (e) CS and (f) CSe. Insets in (e) and (f) show the final geometric structures after AIMD simulation.

  DownLoad: Full-Size Img PowerPoint

  Before moving on to other properties, we first focus on the structural stability of the CX monolayers, including their dynamical, thermal, and mechanical stability. To assess their dynamical stabilities, the phonon dispersion curves are calculated based on the frozen-phonon method as implemented in the PHONOPY package [51]. The 5 × 5 × 1 supercell and 4 × 4 × 1 Γ centered k-point sampling are used for the phonon calculations. As shown in Figs. 1c and d, we find that the low-frequency optical and acoustic modes separate apart from each other around the Γ point, and the frequencies of all phonon modes in the entire Brillouin zone are positive. The highest frequencies of monolayer CS and CSe reach up to 680 cm⁻¹ and 580 cm⁻¹, respectively, which are comparable to those of silicene (550 cm⁻¹) [52] and blue phosephorene (520 cm⁻¹) [53]. These results demonstrate that our proposed two monolayer materials are dynamically stable. Furthermore, we examine their thermal stability by performing ab initio molecular-dynamics (AIMD) simulations at 300 K using a 5 × 5 × 1 supercell. As plotted in Figs. 1e and f, the total energies have small fluctuations and the initial geometric structures are well maintained after 10 ps simulation with the NVT ensemble, suggesting that monolayer CS and CSe can be stable at the room-temperature. In addition, we also investigate the effect of the O₂ molecule on their structural stabilities. As shown in Fig. S2 (Supporting information), we can see that the distances from the O₂ molecule to the CS and CSe monolayers are 2.67 and 2.52 Å, respectively, and the corresponding binding energy (E_a) are 151 meV and 223 meV. This indicates that O₂ molecule is bonded to the monolayers mainly by vdW force. As a result, our proposed CX monolayers can be stable in the presence of O₂.

  Additionally, we systematically examine the elastic properties of the CX monolayers to analyze the mechanical stability. Based on the strain-energy method, the calculated elastic constants of monolayer CS (CSe) are C₁₁ = C₂₂ = 132.64 (95.59) N/m, C₁₂ = 14.69 (16.20) N/m and C₆₆ = 58.97 (39.69) N/m. Clearly, the Born-Huang criteria of mechanical stability for 2D hexagonal materials (e.g., C₁₁C₂₂ - C₁₂² > 0, C₆₆ > 0) is nicely satisfied, reflecting the mechanical robustness of monolayer CS and CSe. Given these elastic constants, we also calculate the in-plane Young's modulus (Y) and Poisson's ratio (υ), which are defined as Y = (C₁₁² - C₁₂²)/C₁₁ and υ = C₁₂/C₁₁, respectively. The in-plane Young's modulus (Y) and Poisson's ratio (υ) of monolayer CS (CSe) are found to be 131.01 (92.84) N/m and 0.11 (0.17), respectively. These results are lower than graphene [54] but comparable to MoS₂ [55], indicate that the bonding between atoms in these two monolayers are strong and would avail to avoid the curling.

  Encouraged by the excellent stability of the CX monolayers, we then turn to discuss their electronic properties by computing the band structures as well as the density of states (DOSs). As shown in Fig. 2, both of CS and CSe monolayers present indirect band gap semiconductor characteristics. The valence band maximum (VBM) of CS monolayer lies at the point between K and Γ points and their conduction band minimum (CBM) is situated at the M point. As for CSe monolayer, the VBM is still located on the K → Γ path while the CBM is located between the Γ and M points. Although a direct gap semiconductor is preferred, the materials with indirect band gaps can also be used as promising photocatalysts for water splitting because they advantageously reduce the recombination possibility of photogenerated electron-hole pairs. On basis of the HSE06 calculation, the predicted band gap values are 2.41 eV for CS and 2.46 eV for CSe. Noted that these values are lower than the band gap of metal-free graphitic carbon nitride (g-C₃N₄), which has been experimentally identified as a visible-light-responsive photocatalyst [56, 57]. From the computed partial DOSs depicted in the Fig. 2, we can see that the VBMs of monolayer CS and CSe are mainly contributed by X 3p, C 2s and C 2p states, while their CBMs are primarily originated from the hybridization of X 3p and C 2p states.

  Figure 2

  

  Figure 2.  HSE06 calculated electronic band structures and projected density of states of monolayer (a) CS and (b) CSe. Here, the Fermi energy levels are scaled to zero and shown as red dashed lines.

  DownLoad: Full-Size Img PowerPoint

  To further explore the charge transport properties for potential energy conversion application, the carrier mobility of CX monolayers are estimated according to the deformation potential (DP) theory proposed by Bardeen and Shockley [58, 59]. The carrier mobility for 2D materials is described as

  (1)

  where e, , and T represent electron charge, reduced Planck constant, Boltzmann constant, room temperature (taken as 300 K), respectively. E_d is the deformation potential constant calculated by dE_edge/dε, in which E_edge is the energy of the conduction (valence) band edge and ε is the applied uniaxial strain. The elastic modulus C_2D is defined as [∂²E/∂ε²]/S₀, where E and S₀ are the total energy under uniaxial strain and the area of the supercell, respectively. m* and m_d represent the effective mass of carrier along the transport direction and average effective mass, respectively, which are determined by and . In our work, the orthogonal supercell, as marked in Fig. 1a with blue solid lines, is adopted to evaluate the carrier mobility of monolayer CS and CSe in a and b directions. The computational details are presented in Figs. S3 and S4 (Supporting information), and the obtained effective mass (m*), elastic modulus (C_2D), deformation potential constant (E_d), and carrier mobility (μ) are summarized in Table 1. It can be observed that CX monolayers exhibit strong electrical transport bias; their hole mobility are substantially higher than the electron mobility in both the a and b directions. This marked difference between the electrons and holes will be propitious to the separation of photoexcited charge carriers and the suppression of electron-hole recombination. It is worth noting that the hole mobility along the b direction are as high as 3.23 × 10⁴ cm² V⁻¹ s⁻¹ for monolayer CS and 4.27 × 10³ cm² V⁻¹ s⁻¹ for monolayer CSe because of the smaller effective mass and deformation potential, which are comparable to or even higher than those of many recently reported 2D photocatalysts, such as MoS₂ (200 cm² V⁻¹ s⁻¹) [60], phosphorene (600−1580 cm² V⁻¹ s⁻¹) [61], and MnPSe₃ (625.9 cm² V⁻¹ s⁻¹) [62]. Such ultrahigh carrier mobility endows the photoexcited electrons and holes to migrate fast from the semiconductor photocatalyst to the active sites. These properties indicate that these CX monolayers are very promising candidates for photocatalytic water splitting.

  Table 1

  

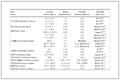  Table 1.  Carrier effective mass (m*), 2D elastic modulus (C_2D), deformation potential (E_d), and carrier mobility (μ) of CX monolayers.

  DownLoad: CSV

  Now, we explore the possibility of using CX monolayers as photocatalysts for water splitting. Owing to the electronegativity difference between C and X atoms, the C atoms in the top layer are negatively charged whereas the X atoms in the bottom layer are positively charged. Thus, an intrinsic dipole (P) is generated, which are found to be 0.43 D for CS and 0.51 D for CSe. As we known, these relatively large dipole can introduce internal electric field (E_eff) in monolayer CX, which are along with the perpendicular plane direction and point from X side to C side. Moreover, as described by the Yang group, the energy levels of the monolayer CS and CSe would bend along the direction of the built-in E_eff, accompanied by the presence of the difference (ΔΦ) between the vacuum energy levels on the two respective sides [26]. As shown in Figs. 3a and b, the top and bottom vacuum regions are different by 2.34 and 2.38 eV for monolayer CS and CSe, respectively, which are as large as some widely known 2D materials with intrinsic electric polarization [27-36], such as MXene, germanium monochalcogenide and Janus metal chalcogenides.

  Figure 3

  

  Figure 3.  Electrostatic potentials of monolayer (a) CS and (b) CSe. Band alignments with respect to the redox potentials of water for monolayer (c) CS and (d) CSe. E_eff represents the internal effective electric field generated by the intrinsic dipole.

  DownLoad: Full-Size Img PowerPoint

  To assess whether monolayer CX possess strong reduction/oxidation ability, we further calculate their accurate VBM/CBM locations by considering the vacuum level corrections, and then align them relative to the redox potential levels for H⁺/H₂ (−4.44 eV at pH 0) and O₂/H₂O (−5.67 at pH 0), which are illustrated in Figs. 3c and d. It should be pointed that the photogenerated electrons and holes can aggregate separately on disparate sides of monolayer CX because of the built-in electric field, meaning that the hydrogen reduction reaction and water oxidation reaction happen on the X and C sides, respectively. On the X atomic layer side, the CBM potentials of CX monolayers (−3.47 eV for CS and −3.12 eV for CSe) lie above hydrogen reduction potential, showing that H⁺ can be reduced to H₂ by the photogenerated electrons. On the C atomic layer side, the VBMs (−8.21 eV for CS and −7.96 eV for CSe) lie below water oxidation potential, showing that H₂O can be oxidized to O₂ by the photogenerated holes. Following a previous study, the energy difference between the CBM and the hydrogen reduction potential is defined as the potential of photogenerated electrons for hydrogen evolution reaction (U_e), while the energy difference between the VBM and the water oxidation potential is calculated as the potential of photogenerated holes for oxygen evolution reaction (U_h). Hence, the U_e and U_h are calculated to be 0.97/2.54 eV for CS and 1.32/2.29 eV for CSe, suggesting that both of them are capable to work as highly efficient photocatalysts for water splitting without using sacrificial reagents or cocatalysts.

  In practical applications for energy storage and conversion, the external strain would inevitably occur and usually play an important role in modulating the properties of 2D photocatalyst materials. As such, we further study the effects of in-plane biaxial strains in the range from −5% to 5% on the electronic structures and photocatalytic properties of monolayer CS and CSe. The biaxial strain is defined as , where a₀ and a are the lattice parameters of nonstrained and strained systems, respectively. The positive value indicates tensile strain, while the negative value denotes compressive strain. Fig. 4 gives the HSE06 calculated band structures of monolayer CX under compression (−1%, −3% and −5%) and tension (1%, 3% and 5%). Comparing with the strain-free cases, we find that the band structure topologies of monolayer CS and CSe at different values of strains are similar except that the CBM of CSe shifts to Γ point with the applied tensile strain larger than 3%. More importantly, the band gaps of monolayer CX can be significantly influenced by the biaxial strain, decreasing with increasing tensile strain and increasing with an increase of compressive strain. The band gaps of monolayer CS/CSe can be reduced to 2.23/1.77 eV under 5% tensile strain and enlarged to 2.71/2.77 eV when the biaxial compressive strain reaches −5%. Such controllable band gap properties of monolayer CX, easily achieved via biaxial strain engineering, would be beneficial for extending the visible-light adsorption.

  Figure 4

  

  Figure 4.  Band structures of monolayer (a) CS and (b) CSe at −5%, −3%, −1%, 1%, 3% and 5% biaxial strain. The Fermi levels (red dashed lines) are set to zero.

  DownLoad: Full-Size Img PowerPoint

  Meanwhile, the dipole moment P and electrostatic potential difference of monolayer CS and CSe are expected to be effectively modulated by applying external biaxial strain. To explore this issue, the variations of the dipole moment and electrostatic potential difference as a function of the biaxial strain are studied. As shown in Fig. 5a, the dipole moment of monolayer CS/CSe slightly decrease with the biaxial strain changing from −5% to 5%, for example, 0.46/0.54 D, 0.45/0.53 D, 0.41/0.50 D and 0.39/0.49 D at −5%, −3%, 3% and 5% strain. The applied strain has similar influences on the electrostatic potential difference of monolayer CX, which can be engineered from 2.48/2.54 eV to 2.12/2.16 eV for the CS and CSe monolayers, respectively. These values under the compressive and tensile strain states are still sufficiently large to induce strong intrinsic electric field, and thus remarkable charge separation can also occur in these strained CX systems.

  Figure 5

  

  Figure 5.  Strain effects on (a) electrostatic potential differences and dipole moments, (b) band edge positions of monolayer CS and CSe.

  DownLoad: Full-Size Img PowerPoint

  To explore the strain effect on the reduction/oxidation ability of monolayer CS and CSe, their band edge alignments as a function of the biaxial strain are further calculated and shown in Fig. 5b. It should be noted that the redox potentials of water splitting depend on the pH value of the solution, which increase with pH by pH × 0.059 eV [63]. Thus, the band edge alignments of the CS and CSe monolayers as well as the reduction/oxidation ability will change in different solution environments. Consequently, the water redox potential at the acidic (pH 0) and neutral environment (pH 7) are computed and plotted in Fig. 5b by light gray and green horizontal dashed lines, respectively. We can see that applying compressive strain makes the U_e and U_h distinctly increase, while they gradually decrease when introducing external tensile strain. More fascinatingly, the CBM energies of all strained monolayer CX systems are higher than the reduction potential of H⁺/H₂ and the corresponding VBM energies are lower than the oxidation potential of O₂/H₂O. The band edge positions are all situated at the favorable positions regardless of acidic or neutral environment, satisfying the requirements of photocatalyst for overall water splitting.

  It is well-known that the light-harvesting performance is also an essential ingredient in determining the photocatalytic efficiency of water splitting. So that, we finally simulate the optical absorption spectrums of monolayer CX systems based on the HSE06 functional. According to the frequency-dependent dielectric function , the optical absorption coefficient α_abs as a function of photon energy can be calculated by using the following equation [64],

  (2)

  where ε₁(ω) and ε₂(ω) are the real and imaginary parts of dielectric function, respectively. Fig. 6 shows the obtained results for monolayer CS and CSe within the strain range of −5%~5%. Here, only the absorption spectrums that the polarization directions are parallel to the planes of monolayer CX are considered. For the CS and CSe monolayers at strain-free states, the optical absorptions can be activated by the incoming light irradiation with photon energies higher than about 2.40 eV, which are coincident with the values of the band gaps obtained in pervious calculations. Moreover, they exhibit strong light absorption in both the ultraviolet and visible-light region, and the absorption intensities are as large as about 10⁵ cm⁻¹. As for monolayer CX systems under compressive strains, blue-shifted absorption edges in their absorption spectrums are observed, which are due to their larger band gaps. However, when the biaxial tensile strains are applied at monolayer CS and CSe, the absorption curves are considerably extended toward the visible-light region because of the narrowing of band gaps. These above results indicate that our proposed CX monolayers have outstanding absorption behaviours and can absorb as much visible-light as possible by tensile strain engineering, suggesting that they are promising metal-free photocatalyst for visible-light-driven water splitting.

  Figure 6

  

  Figure 6.  Optical absorption spectrums of monolayer (a) CS and (b) CSe within the strain range of −5% to 5%.

  DownLoad: Full-Size Img PowerPoint

  For the practical application of photocatalytic water splitting, of course require the semiconductor material to be hydrophilic, which is another significant parameter characterizing its performance. To investigate how strong the interactions are between the H₂O molecule and our proposed CX monolayers, several possible adsorption configurations are considered and geometrically optimized. The most energetically favorable configurations for H₂O molecule adsorbed on CX monolayers are shown in Fig. S5 (Supporting information). The distances from the H₂O molecule to the CS and CSe monolayers are 2.29 and 2.09 Å, respectively, and the corresponding binding energy (E_a) are 191 meV and 235 meV. The relatively large E_a suggests a strong interaction between the H₂O molecule and the monolayers, ensuring better photocatalytic water-splitting activity.

  In conclusion, by performing first-principles calculations, we systematically investigate the structural, electronic and photocatalytic properties of blue-phase CX (X = S, Se) monolayers. From the calculated phonon spectrums and elastic constants as well as AIMD simulations, we first verify that the proposed CX monolayers are dynamically, thermally, and mechanical stable. Then, CS and CSe monolayers are found to be indirect semiconductors with band gap of 2.41 and 2.46 eV, respectively. The calculated hole mobility along the b direction can be as high 3.23 × 10⁴ cm² V⁻¹ s⁻¹ for CS and 4.27 × 10³ cm² V⁻¹ s⁻¹ for CSe, which are comparable to those of many recently reported 2D photocatalysts. Furthermore, internal electrical fields are induced in these predicted monolayer materials due to the large intrinsic dipole, reducing the possibility of electron-hole recombination. More fascinatingly, CS and CSe monolayers not only possess favorable band edge positions with respect to water redox potentials and but also have strong capacity of optical absorption with the intensity up to 10⁵ cm^-1. Finally, we find that applying external strain can further adjust the band gaps, band alignments, and optical absorption behaviours of CX monolayers. These theoretical findings suggest that our proposed CS and CSe monolayers have great potential in the field of photocatalytic water splitting.

  Declaration of competing interest

  The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

  Acknowledgments

  This work was partially supported by the National Natural Science Foundation of China (No. 21503149), by the Program for Innovative Research Team in University of Tianjin (No. TD13-5074), by the Project of Hubei University of Arts and Science (Nos. xk2020043, xk2020044, 2020kypyfy015).

  Appendix A. Supplementary data

  Supplementarymaterial related to this article canbefound, in the online version, at doi:https://doi.org/10.1016/j.cclet.2020.09.056.

  
  
• 1. [1]

     Q. Wang, K. Domen, Chem. Rev. 120 (2020) 919-985. doi: 10.1021/acs.chemrev.9b00201

  2. [2]

     C. Dong, J. Ji, Z. Yang, et al., Chin. Chem. Lett. 30 (2019) 853-862. doi: 10.1016/j.cclet.2019.03.020

  3. [3]

     J. Wang, J. Huang, J. Meng, et al., RSC Adv. 7 (2017) 39877-39884. doi: 10.1039/C7RA03175K

  4. [4]

     M. Zeng, L. Zhang, D. Wu, et al., Chin. Chem. Lett. 30 (2019) 1329-1334. doi: 10.1016/j.cclet.2019.01.026

  5. [5]

     A. Fujishima, K. Honda, Nature 238 (1972) 37-38. doi: 10.1038/238037a0

  6. [6]

     Y. Yang, S. Niu, D. Han, et al., Adv. Energy Mater. 7 (2017) 1700555. doi: 10.1002/aenm.201700555

  7. [7]

     J. Huang, R. Xie, Y. Hu, et al., Chem. Phys. Lett. 758 (2020) 137925. doi: 10.1016/j.cplett.2020.137925

  8. [8]

     J. Wang, J. Teng, L. Pu, et al., Int. J. Quantum Chem. 119 (2019) e25930. doi: 10.1002/qua.25930

  9. [9]

     Z. Wang, C. Li, K. Domen, Chem. Soc. Rev. 48 (2019) 2109-2125. doi: 10.1039/C8CS00542G

  10. [10]

      L. Cheng, Q. Xiang, Y. Liao, et al., Energy Environ. Sci. 11 (2018) 1362-1391. doi: 10.1039/C7EE03640J

  11. [11]

      Y. Sun, T. Zhang, C. Li, et al., J. Mater. Chem. A: Mater. Energy Sustain. 8 (2020) 13415-13436. doi: 10.1039/D0TA05038E

  12. [12]

      Y. Yang, Y. Tang, H. Jiang, et al., Chin. Chem. Lett. 30 (2019) 2089-2109. doi: 10.1016/j.cclet.2019.10.041

  13. [13]

      C. -F. Fu, X. Wu, J. Yang, Adv. Mater. 30 (2018) 1802106. doi: 10.1002/adma.201802106

  14. [14]

      X. Zhou, H. Dong, ChemCatChem 11 (2019) 3688-3715. doi: 10.1002/cctc.201900567

  15. [15]

      J. Wang, M. Zhang, J. Meng, et al., RSC Adv. 7 (2017) 24446-24452. doi: 10.1039/C7RA01723E

  16. [16]

      Y. Zhao, S. Zhang, R. Shi, et al., Mater. Today 34 (2020) 78-91. doi: 10.1016/j.mattod.2019.10.022

  17. [17]

      L. Zhao, Y. Li, G. Zhou, et al., Chin. Chem. Lett. 32 (2021) 900-905. doi: 10.1016/j.cclet.2020.07.016

  18. [18]

      J. Wang, X. Yang, J. Cao, et al., Comput. Mater. Sci. 150 (2018) 432-438. doi: 10.1016/j.commatsci.2018.04.049

  19. [19]

      F. Yu, L. Wang, Q. Xing, et al., Chin. Chem. Lett. 31 (2020) 1648-1653. doi: 10.1016/j.cclet.2019.08.020

  20. [20]

      S. Zhao, R. Nivetha, Y. Qiu, et al., Chin. Chem. Lett. 31 (2020) 947-952. doi: 10.1016/j.cclet.2019.11.045

  21. [21]

      Y. Wan, L. Wang, H. Xu, et al., J. Am. Chem. Soc. 142 (2020) 4508-4516. doi: 10.1021/jacs.0c00564

  22. [22]

      Y. Yang, M. Wu, X. Zhu, et al., Chin. Chem. Lett. 30 (2019) 2065-2088. doi: 10.1016/j.cclet.2019.11.001

  23. [23]

      Y. Sun, H. Cheng, S. Gao, et al., Angew. Chem. Int. Ed. 51 (2012) 8727-8731. doi: 10.1002/anie.201204675

  24. [24]

      Z. Cheng, T.A. Shifa, F. Wang, et al., Adv. Mater. 30 (2018) 1707433. doi: 10.1002/adma.201707433

  25. [25]

      M. Qiao, J. Liu, Y. Wang, et al., J. Am. Chem. Soc. 140 (2018) 12256-12262. doi: 10.1021/jacs.8b07855

  26. [26]

      X. Li, Z. Li, J. Yang, Phys. Rev. Lett. 112 (2014) 018301. doi: 10.1103/PhysRevLett.112.018301

  27. [27]

      Y. Ji, M. Yang, H. Lin, et al., J. Phys. Chem. C 122 (2018) 3123-3129. doi: 10.1021/acs.jpcc.7b11584

  28. [28]

      R. Peng, Y. Ma, B. Huang, et al., J. Mater. Chem. A: Mater. Energy Sustain. 7 (2019) 603-610. doi: 10.1039/C8TA09177C

  29. [29]

      C. Xia, W. Xiong, J. Du, et al., Phys. Rev. B 98 (2018) 165424. doi: 10.1103/PhysRevB.98.165424

  30. [30]

      W. Chen, X. Hou, X. Shi, et al., ACS Appl. Mater. Interfaces 10 (2018) 35289-35295. doi: 10.1021/acsami.8b13248

  31. [31]

      C.F. Fu, X. Li, Q. Luo, et al., J. Mater. Chem. A Mater. Energy Sustain. 5 (2017) 24972-24980. doi: 10.1039/C7TA08812D

  32. [32]

      A. Huang, W. Shi, Z. Wang, J. Phys. Chem. C 123 (2019) 11388-11396. doi: 10.1021/acs.jpcc.8b12450

  33. [33]

      R. da Silva, R. Barbosa, R.R. Mancano, et al., ACS Appl. Nano Mater. 2 (2019) 890-897. doi: 10.1021/acsanm.8b02135

  34. [34]

      Z. Wang, G. Zhou, J. Phys. Chem. C 124 (2020) 167-174. doi: 10.1021/acs.jpcc.9b09914

  35. [35]

      C.F. Fu, J. Sun, Q. Luo, et al., Nano Lett. 18 (2018) 6312-6317. doi: 10.1021/acs.nanolett.8b02561

  36. [36]

      P. Zhao, Y. Ma, X. Lv, et al., Nano Energy 51 (2018) 533-538. doi: 10.1016/j.nanoen.2018.07.010

  37. [37]

      C. Chowdhury, S. Karmakar, A. Datta, J. Phys. Chem. C 121 (2017) 7615-7624. doi: 10.1021/acs.jpcc.6b12080

  38. [38]

      J.R. Brent, D.J. Lewis, T. Lorenz, et al., J. Am. Chem. Soc. 137 (2015) 12689-12696. doi: 10.1021/jacs.5b08236

  39. [39]

      J. Wang, S. Li, F. Yun, et al., Int. J. Quantum Chem. 120 (2020) e26230.

  40. [40]

      Z. Zhu, J. Guan, D. Liu, et al., ACS Nano 9 (2015) 8284-8290. doi: 10.1021/acsnano.5b02742

  41. [41]

      Y. Ji, M. Yang, H. Dong, et al., Nanoscale 9 (2017) 8608-8615. doi: 10.1039/C7NR00688H

  42. [42]

      Y.L. Zhu, J.H. Yuan, Y.Q. Song, et al., J. Mater. Sci. 54 (2019) 11485-11496. doi: 10.1007/s10853-019-03699-y

  43. [43]

      L. Sun, Y. Cui, L. Peng, et al., J. Catal. 373 (2019) 67-74. doi: 10.1016/j.jcat.2019.03.031

  44. [44]

      D. Gu, X. Tao, H. Chen, et al., Nanoscale 11 (2019) 2335-2342. doi: 10.1039/C8NR08908F

  45. [45]

      P.E. Blöchl, Phys. Rev. B 50 (1994) 17953. doi: 10.1103/PhysRevB.50.17953

  46. [46]

      G. Kresse, J. Furthmüller, Phys. Rev. B 54 (1996) 11169. doi: 10.1103/PhysRevB.54.11169

  47. [47]

      J.P. Perdew, K. Burke, M. Ernzerhof, Phys. Rev. Lett. 77 (1996) 3865. doi: 10.1103/PhysRevLett.77.3865

  48. [48]

      J. Heyd, G.E. Scuseria, M. Ernzerhof, J. Chem. Phys. 118 (2003) 8207-8215. doi: 10.1063/1.1564060

  49. [49]

      J. Heyd, G.E. Scuseria, M. Ernzerhof, J. Chem. Phys. 124 (2006) 219906. doi: 10.1063/1.2204597

  50. [50]

      H.J. Monkhorst, J.D. Pack, Phys. Rev. B 13 (1976) 5188. doi: 10.1103/PhysRevB.13.5188

  51. [51]

      A. Togo, I. Tanaka, Scr. Mater. 108 (2015) 1-5. doi: 10.1016/j.scriptamat.2015.07.021

  52. [52]

      X.J. Ge, K.L. Yao, J.T. Lü, Phys. Rev. B 94 (2016) 165433. doi: 10.1103/PhysRevB.94.165433

  53. [53]

      Z. Zhu, D. Tománek, Phys. Rev. Lett. 112 (2014) 176802. doi: 10.1103/PhysRevLett.112.176802

  54. [54]

      R.C. Andrew, R.E. Mapasha, A.M. Ukpong, et al., Phys. Rev. B 85 (2012) 125428. doi: 10.1103/PhysRevB.85.125428

  55. [55]

      R.C. Cooper, C. Lee, C.A. Marianetti, et al., Phys. Rev. B 87 (2013) 035423. doi: 10.1103/PhysRevB.87.035423

  56. [56]

      J. Wang, Z. Guan, J. Huang, et al., J. Mater. Chem. A: Mater. Energy Sustain. 2 (2014) 7960-7966. doi: 10.1039/C4TA00275J

  57. [57]

      J. Wang, X. Li, Y. You, et al., Nanotechnology 29 (2018) 365401. doi: 10.1088/1361-6528/aace20

  58. [58]

      J. Bardeen, W. Shockley, Phys. Rev. 80 (1950) 72-80. doi: 10.1103/PhysRev.80.72

  59. [59]

      J. Qiao, X. Kong, Z.X. Hu, et al., Nat. Commun. 5 (2014) 4475. doi: 10.1038/ncomms5475

  60. [60]

      Y. Cai, G. Zhang, Y. -W. Zhang, J. Am. Chem. Soc. 136 (2014) 6269-6275. doi: 10.1021/ja4109787

  61. [61]

      J. Xiao, M. Long, X. Zhang, et al., Sci. Rep. 5 (2015) 9961. doi: 10.1038/srep09961

  62. [62]

      X. Zhang, X. Zhao, D. Wu, et al., Adv. Sci. 3 (2016) 1600062. doi: 10.1002/advs.201600062

  63. [63]

      J. Wang, J. Meng, Q. Li, et al., Phys. Chem. Chem. Phys. 18 (2016) 17029-17036. doi: 10.1039/C6CP01001F

  64. [64]

      M. Gajdoš, K. Hummer, G. Kresse, et al., Phys. Rev. B 73 (2006) 45112-45120. doi: 10.1103/PhysRevB.73.045112

• 

  Figure 1  (a) Geometric structure of CX monolayers from thetop and side views. The hexagonal primitive cell and orthogonal supercell are marked by black and blue lines, respectively. (b) Visualization of the electron localization function for monolayer CS. Calculated phonon dispersions of monolayer (c) CS and (d) CSe. The total energy fluctuations during 10 ps AIMD simulations at room temperature (300 K) for monolayer (e) CS and (f) CSe. Insets in (e) and (f) show the final geometric structures after AIMD simulation.

  下载: 全尺寸图片 幻灯片
  

  Figure 2  HSE06 calculated electronic band structures and projected density of states of monolayer (a) CS and (b) CSe. Here, the Fermi energy levels are scaled to zero and shown as red dashed lines.

  下载: 全尺寸图片 幻灯片
  

  Figure 3  Electrostatic potentials of monolayer (a) CS and (b) CSe. Band alignments with respect to the redox potentials of water for monolayer (c) CS and (d) CSe. E_eff represents the internal effective electric field generated by the intrinsic dipole.

  下载: 全尺寸图片 幻灯片
  

  Figure 4  Band structures of monolayer (a) CS and (b) CSe at −5%, −3%, −1%, 1%, 3% and 5% biaxial strain. The Fermi levels (red dashed lines) are set to zero.

  下载: 全尺寸图片 幻灯片
  

  Figure 5  Strain effects on (a) electrostatic potential differences and dipole moments, (b) band edge positions of monolayer CS and CSe.

  下载: 全尺寸图片 幻灯片
  

  Figure 6  Optical absorption spectrums of monolayer (a) CS and (b) CSe within the strain range of −5% to 5%.

  下载: 全尺寸图片 幻灯片

  Table 1.  Carrier effective mass (m*), 2D elastic modulus (C_2D), deformation potential (E_d), and carrier mobility (μ) of CX monolayers.

  下载: 导出CSV
•