English

• 稀土离子掺杂上转换发光材料由于具有广阔的应用前景引起了人们极大的兴趣，其中Er离子具有丰富的能级结构，可以很容易被低成本近红外附近的激光器激发产生从紫外到红外很宽波段的光发射，因此被广泛报道^[1-4]。为了获得高性能的稀土Er掺杂上转换发光材料，Yb离子通常被添加作为Er离子的敏化剂，这是由于Yb离子具有特殊的能级结构和较长的激发态寿命^[5-7]。除了选择合适的敏化剂，Er离子掺杂上转换发光材料基质的选取对其发光性能也十分重要。氟化物由于具有低的声子能量作为Er离子掺杂基质材料被广泛研究，目前被广泛看好且研究较多的是β相NaYF₄体系，并已被应用于生物医学成像、疾病诊断和传感器等^[8-10]。一般认为2% Er³⁺-20% Yb³⁺(物质的量分数)共掺杂β相NaYF₄纳米晶具有很高的上转换发光效率^[11-15]。相对于氟化物基质材料，氧化物由于具有良好的化学稳定性和力学特性近年来也受到人们的重视^[16-17]。针对浓度优化的研究有很多，但这些工作都存在着各自的问题。试验优化设计是一种比较科学的设计方法，可以通过尽量少的实验来获取尽可能多的信息，能够客观、科学地选取实验点，实现方案设计、试验实施和数据处理全过程的最优化^[18-20]。在Er掺杂上转换发光材料中，氧化物Gd₂Ti₂O₇基质具有较高的化学稳定性、机械强度以及高温稳定性，由于Er³⁺、Yb³⁺和Gd³⁺离子半径相近能够相互取代，使得Er³⁺和Yb³⁺离子能够大浓度均匀掺杂到Gd₂Ti₂O₇基质中且不改变其相结构。本文采用溶胶-凝胶(Sol-gel)法制备Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇纳米晶粉末，通过试验优化设计理论建立Er³⁺-Yb³⁺掺杂浓度与发光强度的回归方程，并利用遗传算法计算出方程的最优解Er³⁺、Yb³⁺的掺杂浓度。对Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇粉末的相结构和上转换发光进行了表征，研究了最优样品上转换发光的温度依赖特性，并探讨了绿色上转换发光的温度传感特性和红色上转换发光的温度猝灭效应。

  1   实验部分

  1.1   原料与试剂

  实验所用化学药品硝酸铒(Er(NO₃)₃·5H₂O，99.9%)、硝酸镱(Yb(NO₃)₃·5H₂O，99.9%)和硝酸钆(Gd(NO₃)₃·6H₂O，99.9%)购于阿拉丁试剂（上海）有限公司。所用试剂钛酸正丁酯(Ti(OBu)₄，分析纯)、乙酰丙酮(acac，分析纯)、异丙醇((CH₃)₂CHOH，分析纯)和硝酸(HNO₃，分析纯)购于国药集团化学试剂有限公司。

  1.2   均匀设计

  采用以前报道过的Sol-gel法制备Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇纳米晶粉末^[21]。将Ti(OBu)₄和acac混合搅拌1 h，室温下加入一定量异丙醇作为溶剂，然后缓慢滴加去离子水与少量异丙醇的混合液，为了进一步控制Ti(OBu)₄的水解和缩聚反应速度再滴加适量HNO₃，持续搅拌4 h，随后按照表 1给出的掺杂浓度向上述溶液中加入Er(NO₃)₃·5H₂O、Yb(NO₃)₃·5H₂O和Gd(NO₃)₃·6H₂O，搅拌4 h得到透明溶胶。其中Ti(OBu)₄、acac、H₂O和HNO₃之间的物质的量比为3:3:6:1，Er³⁺、Yb³⁺、Gd³⁺和Ti⁴⁺的物质的量比为x₁:x₂:(1-x₁-x₂):1。获得的溶胶在373 K干燥12 h，烘干成凝胶，放入热处理炉中以20 K·min^-1的升温速率在1 523 K保温1 h，随炉冷却至室温后研磨即得Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇纳米晶粉末。

  表 1  均匀设计实验 Table 1.  Uniform experimental design

  表选项

  导出Excel

  下载全尺寸表图像

  Number	Factor
  	Er3+x1 / %	Yb3+x2 / %	yred
  1	1(1.000)	4(34.125)	20 472.0
  2	2(2.000)	8(79.625)	811.2
  3	3(3.000)	3(22.750)	144 563.7
  4	4(4.000)	7(68.250)	1 590.3
  5	5(5.000)	2(11.375)	249 612.0
  6	6(6.000)	6(56.875)	3 638.5
  7	7(7.000)	1(0.000)	4 011.1
  8	8(8.000)	5(45.500)	5 487.8
  9	9(9.000)	9(91.000)	2 947.2

  采用波长为976 nm的半导体激光器(LD)作为泵浦光源，通过Jobin Yvon iHr550型单色仪和CR131光电倍增管对样品的上转换发光光谱进行采集，测试9个样品的上转换发射光谱，并对红色上转换发光部分积分。如表 1第四列所示，5号样品的发光强度最大，对应Er³⁺和Yb³⁺的掺杂浓度分别为5.000%和11.375%。以该组样品的Er³⁺/Yb³⁺掺杂浓度为参考，确定二次通用旋转组合设计中Er³⁺/Yb³⁺的掺杂浓度范围分别为3.000%~7.000%和0%~20.000%。

  1.3   二次通用旋转组合设计

  根据均匀设计确定的Er³⁺/Yb³⁺离子浓度范围，进行二次通用旋转组合设计。由于二次通用旋转组合设计只有在编码空间中才具有通用性、旋转性等优异性质，符合建模和检验的要求，所以先将因素进行编码。表 2为自然因素水平编码表，选取了Er³⁺/Yb³⁺掺杂浓度的5个水平，编码水平分别为±r、±1和0。表 3为二次通用旋转组合设计实验的方案及结果，最后一列所示为13组样品的红光部分的积分强度。其中每个编码对应的离子浓度如表 2所示，共进行13组实验。

  表 2  自然因素水平编码表 Table 2.  Natural factors level code

  表选项

  导出Excel

  下载全尺寸表图像

  zj(xj)	z1(Er3+) / %	z2(Yb3+) / %
  z2j(r)	7	20
  z0j+Δj(1)	6.414	17.072
  z0j(0)	5	10
  z0j-Δj(-1)	3.586	2.928
  z1j(-r)	3	0
  Δj=(z2j-z1j)/(2r)	1.414	7.072
  xj=(zj-z0j)Δj	xj=(zj-5)/1.414	xj=(Zj-10)/7.072

  表 3  二次通用旋转组合设计的实验方案与积分强度的结果表 Table 3.  Integrated intensity and experiment scheme of quadratic general rotary unitized design

  表选项

  导出Excel

  下载全尺寸表图像

  Number	Factor
  	x0	x1	x2	x1x2	x12	x22	yred
  1	1	1	1	1	1	1	190 597.4
  2	1	1	-1	-1	1	1	77 864.2
  3	1	-1	1	-1	1	1	162 591.9
  4	1	-1	-1	1	1	1	42 600.0
  5	1	r	0	0	r2	0	171 357.2
  6	1	-r	0	0	r2	0	195 836.9
  7	1	0	r	0	0	r2	144 919.0
  8	1	0	-r	0	0	r2	4 406.6
  9	1	0	0	0	0	0	209 290.1
  10	1	0	0	0	0	0	193 202.4
  11	1	0	0	0	0	0	193 850.4
  12	1	0	0	0	0	0	181 725.9
  13	1	0	0	0	0	0	192 503.6

  1.4   样品的表征和性能测试

  采用SHIMADZU XRD-6000型X射线衍射仪(XRD)分析Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇纳米晶粉末的晶体结构，测试条件为Cu Kα辐射(λ=0.154 nm)，所用电压40 kV，电流30 mA，扫描范围10°~80°，扫描速度4°·min^-1。采用波长为976 nm的半导体激光器(LD)作为泵浦光源，通过Jobin Yvon iHr550型单色仪和CR131光电倍增管对样品的上转换发光光谱进行采集。通过实验室自制的小型加热炉对样品进行加热，并通过热电偶和温控仪表对样品温度进行调控，样品以25 K·min^-1的升温速率在相应温度下保温10 min。

  2   结果与讨论

  2.1   二次通用旋转组合设计合成样品表征

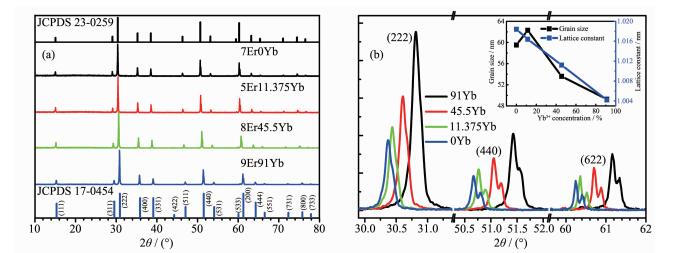
  图 1(a)给出了Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇纳米晶粉末的XRD图。Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇纳米晶粉末为单一面心立方Gd₂Ti₂O₇相结构(JCPDS No.23-0259)，无其它相衍射峰出现。由于Er³⁺、Yb³⁺和Gd³⁺离子半径相近，Er₂T_i2O₇、Yb₂Ti₂O₇和Gd₂Ti₂O₇结构相同且晶格常数相近，因此Er³⁺、Yb³⁺以置换Gd³⁺的形式存在于Gd₂Ti₂O₇晶格中。由于Er³⁺(0.088 nm)和Yb³⁺(0.086 nm)的离子半径比Gd³⁺(0.094 nm)小，Gd³⁺被Er³⁺和Yb³⁺取代能够引起晶格收缩，使得衍射峰向高角偏移。当Er³⁺、Yb³⁺浓度为9和91%(Gd³⁺浓度为0) 时，Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇(Er³⁺掺杂Yb₂Ti₂O₇)的衍射峰可以很好的和Yb₂Ti₂O₇(JCPDS No.17-0454) 一一对应。为更清楚的展现Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇纳米晶粉末衍射峰的位置和宽度，图 1(b)给出了Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇纳米晶粉末的3个主要衍射峰。随Yb³⁺含量的逐渐增多，衍射峰逐渐向高角偏移。衍射峰偏移现象说明在本试验中，Er³⁺、Yb³⁺和Gd³⁺离子可以以任意比例组合成(Er_x1Yb_x2Gd_1-x1-x2)Ti₂O₇这种晶格。不同含量的Er³⁺、Yb³⁺并未引起其他相结构出现。当Er³⁺、Yb³⁺浓度为7%和0%时，Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇(Er³⁺掺杂Gd₂Ti₂O₇)的衍射峰可以和Gd₂Ti₂O₇(JCPDS No.23-0259) 一一对应。图 1(b)插图给出了基质晶格常数和晶粒尺寸随Yb³⁺掺杂浓度的变化关系。随Yb³⁺掺杂浓度逐渐增大，Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇的晶格常数线性降低。根据谢乐公式计算得到的Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇粉末晶粒尺寸随Yb³⁺浓度增加先增大后减小，当Yb³⁺掺杂浓度为11.375%时获得最大晶粒尺寸为62.3 nm。

  图 1  (a) Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇纳米晶粉末的XRD图; (b)纳米晶粉末的主要衍射峰，插图为晶格常数和晶粒尺寸随Yb³⁺掺杂浓度的变化关系 Figure 1.  (a) XRD patterns of Er³⁺-Yb³⁺ co-doped Gd₂Ti₂O₇; (b) Main diffraction peaks of the powder

  图选项

  下载全尺寸图像

  下载幻灯片

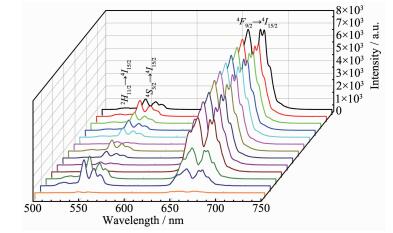
  图 2为二次通用旋转组合设计中13组样品的上转换发光光谱图，各样品发光强度按从高到低分别对应为9、6、11、10、13、1、12、5、3、7、2、4、8号样品。在976 nm LD激发下，Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇获得了分别对应于Er³⁺的²H_11/2/⁴S_3/2→⁴I_15/2和⁴F_9/2→⁴I_15/2跃迁的绿色和红色上转换发光。Er³⁺、Yb³⁺掺杂浓度的变化不改变Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇上转换发光的发射波段，但对其上转换发光强度具有显著影响。

  图 2  Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇的上转换发光光谱 Figure 2.  Upconversion emission spectra of Er³⁺-Yb³⁺co-doped Gd₂Ti₂O₇

  图选项

  下载全尺寸图像

  下载幻灯片

  2.2   二次通用旋转组合设计合成样品数据分析

  根据实验结果可初步建立在编码空间中的回归方程：

  用T-检验及F-检验对方程的回归系数及回归方程进行显著性检验。计算所得各数据如表 4所示。回归系数的T-检验结果表明，各回归系数均在不同程度上显著，在编码空间中Er³⁺/Yb³⁺掺杂浓度与红光发光强度的二次回归方程可简化为：

  表 4  红光的T-检验及F-检验方差分析表 Table 4.  T-test and F-test with analysis of variance of red light

  表选项

  导出Excel

  下载全尺寸表图像

  Source of variance	Sum of square of deviations	Degree of freedom	T statistics and F ratio	Significance level (α)	Significance
  x0	188 402 148 575.5	1	27.324	0.001	****
  x1	102 640 109.4	1	0.638	0.6	Insignificant
  x2	23 264 302 986.2	1	9.601	0.001	****
  x1x2	13 172 163.3	1	0.228	0.9	Insignificant
  x12	427 310 576.6	1	1.301	0.3	Insignificant
  x22	26 996 053 801.8	1	10.340	0.001	****
  0rthogonal	50 667 839 069.6	5	40.157	0.01	****
  Residual	1 766 450 041.9	7	—	—	—
  Fidelity of simulation	1 379 177 538.3	3	4.748	0.01	—
  Error	387 272 503.5	4	—	—	—
  Sum	52 434 289 111.4	12	—	—	—
  Note: **** very significant level (α≤0.01); *** significant level (α≤0.1); ** quiet significant level (α≤0.25)

  回归方程F-检验的显著性水平α＜0.01，说明回归方程的置信度为99%，回归方程失拟检验的显著性水平α＜0.01，获得的回归方程不失拟，说明该模型与实际试验拟合较好，可用于获得最大发光强度的Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇上转换发光纳米晶粉末的理论预测。将编码空间中的方程转换到实际空间中，得到在实际空间中Er³⁺/Yb³⁺掺杂浓度与红光发光强度的二次回归方程：

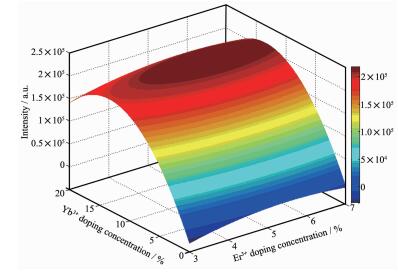
  通过遗传算法求解出方程的最大解，分别对应最优样品的Er³⁺/Yb³⁺掺杂浓度为z₁=5.600，z₂=13.430，并按照求解出的参数制备出相应样品，经测试该样品实际发光强度与理论值非常接近。根据回归方程得到实验区间内的发光强度随Er³⁺/Yb³⁺共掺杂浓度变化的三维立体图，如图 3。

  图 3  红光发光强度随Er³⁺/Yb³⁺共掺杂浓度变化图 Figure 3.  Dependence of red emission intensity on the Er³⁺/Yb³⁺ co-doped concentration

  图选项

  下载全尺寸图像

  下载幻灯片

  2.3   最大发光强度样品的上转换发光机制

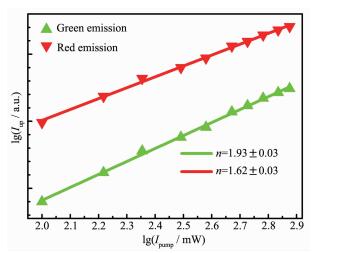
  图 4给出了最优样品的Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇纳米晶粉末的绿色和红色上转换发光强度随泵浦激光功率的变化曲线。对于未饱和的上转换过程，泵浦到高能级所需的光子数满足I_up∝I_pumpⁿ，其中I_up为上转换发光强度，I_pump为激光泵浦功率，n为所需的光子数^[22]。由图可见绿色和红色上转换发光的直线斜率分别为1.93和1.62，表明Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇的绿色和红色上转换发光为双光子吸收过程。

  图 4  Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇上转换发光强度随泵浦激光功率的变化 Figure 4.  Log-log plots of upconversion emissions for Er³⁺-Yb³⁺ co-doped Gd₂Ti₂O₇ versus excitation power of pump laser

  图选项

  下载全尺寸图像

  下载幻灯片

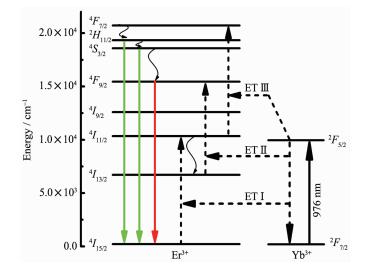
  图 5给出了Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇纳米晶粉末的上转换发光能级图。在976 nm LD激发下，Yb³⁺离子吸收光子能量从基态²F_7/2能级跃迁至激发态²F_5/2能级，然后再以能量传递(ET)的方式将能量传递给Er³⁺。Er³⁺离子通过ET(Ⅰ)和ET(Ⅲ)过程在能级⁴F_7/2上进行布居，随后通过无辐射弛豫至能级²H_11/2和⁴S_3/2后向⁴I_15/2辐射跃迁，发出中心波长524和545 nm的绿色上转换发光。Er³⁺离子通过ET(Ⅰ)、ET(Ⅱ)和无辐射弛豫过程以及⁴S_3/2到⁴F_9/2能级的无辐射弛豫导致能级⁴F_9/2上的布居，然后⁴F_9/2向⁴I_15/2能级辐射跃迁发出中心波长660 nm的红光。上述机制中描述的绿光和红光的双光子过程与图 3的实验结果是一致的。

  图 5  Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇的上转换发光能级图 Figure 5.  Schematic energy levels diagram of Er³⁺-Yb³⁺ co-doped Gd₂Ti₂O₇ powder

  图选项

  下载全尺寸图像

  下载幻灯片

  2.4   最大发光强度样品的温度依赖特性

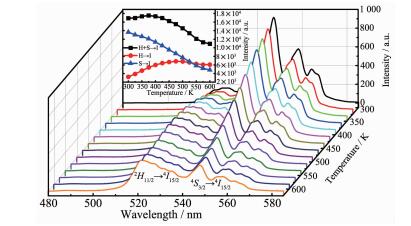
  图 6给出了最优样品的绿色上转换发光随温度的变化关系。随样品温度的升高，上转换发射峰的位置并没有发生改变，而强度变化明显。由插图可知，绿色上转换发光强度随温度升高先缓慢增大随后逐渐减小，对应于²H_11/2→⁴I_15/2跃迁的绿光先增大后略有减小，对应于⁴S_3/2→⁴I_15/2跃迁的绿光强度一直减小。上转换发光强度随温度变化主要受吸收截面和无辐射弛豫过程影响。较低温度时，吸收截面随温度升高而增大，导致绿色上转换发光随温度逐渐增强。当温度较高时，无辐射弛豫速率随温度升高而逐渐增大，引起绿色发光强度随温度逐渐减小^[23]。

  图 6  Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇最优样品的绿色上转换发光随温度的变化关系图 Figure 6.  Green upconversion emissions for Er³⁺-Yb³⁺ co-doped Gd₂Ti₂O₇ versus temperature

  图选项

  下载全尺寸图像

  下载幻灯片

  由于能级²H_11/2和⁴S_3/2处于一个热平衡状态并满足玻尔兹曼分布，因此²H_11/2→⁴I_15/2与⁴S_3/2→⁴I_15/2的发射强度比R可满足关系式^[24]：

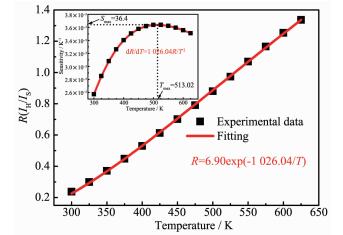
  其中，I_H和I_S分别代表²H_11/2→⁴I_15/2和⁴S_3/2→⁴I_15/2的发射强度，C为常数，ΔE表示²H_11/2和⁴S_3/2之间的能级差，k为玻尔兹曼常数，T表示绝对温度。图 7给出了最优样品的绿色上转换发光强度比R与温度之间的函数关系图。由图可见，²H_11/2→⁴I_15/2与⁴S_3/2→⁴I_15/2发射强度比R和温度T可以很好的拟合成关系式R=6.90exp(-1 026.04/T)。灵敏度是光学温度传感器一个很重要的指标，灵敏度S可以表示为:

  图 7  绿色上转换发光强度比R(I_H/I_S)与温度之间的函数关系图 Figure 7.  Green upconversion emissions ratio of R(I_H/I_S) as a function of temperature

  图选项

  下载全尺寸图像

  下载幻灯片

  图 7插图给出了灵敏度与温度的函数关系。由图可得，在513.02 K时Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇纳米晶粉末可获得最大灵敏度，约为0.00 364 K^{-1 [21]}。

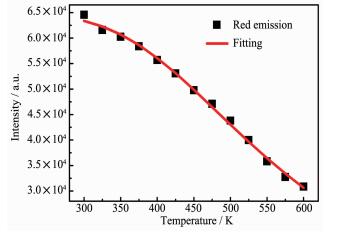
  图 8给出了最优样品的红色上转换发光随温度的变化关系。由图可知，随着温度的升高，红色上转换发光的发射强度逐渐变小，出现了温度猝灭现象。根据Cross over热猝灭理论公式可表示为^[25]:

  图 8  Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇最优样品的红色上转换发光随温度的变化关系图 Figure 8.  Red upconversion emissions for Er³⁺-Yb³⁺ co-doped Gd₂Ti₂O₇ versus temperature

  图选项

  下载全尺寸图像

  下载幻灯片

  式中，I₀是初始强度，I(T)是一个给定温度的强度，A是辐射跃迁的频率因子，ΔE′是热猝灭过程的激活能。用上式对数据进行拟合，求解出最优样品的红色上转换发光的激活能为ΔE'=0.205 eV^[26-27]。

  3   结论

  采用较简单的溶胶-凝胶法制备了不同Er³⁺-Yb³⁺共掺杂浓度的Gd₂Ti₂O₇纳米晶粉末。通过试验优化设计理论中的均匀设计和二次通用旋转组合设计建立了Er³⁺-Yb³⁺掺杂浓度与发光强度的回归方程，利用遗传算法优化计算出方程的最优解Er³⁺、Yb³⁺掺杂浓度分别为5.60%和13.43%，并按照该掺杂浓度制备出相应样品，经测试该样品实际发光强度与理论值非常接近。在976 nm半导体激光器激发下，Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇获得了分别对应于Er³⁺的²H_11/2/⁴S_3/2→⁴I_15/2和⁴F_9/2→⁴I_15/2跃迁的绿色和红色上转换发光，且绿色和红色上转换发光均为双光子吸收过程。研究了最优样品的绿色上转换发光的温度传感性质，求解出最大灵敏度，对红色上转换发光的温度猝灭机理进行了解释。

• 1. [1]

     Dong B, Cao B S, He Y Y, et al. Adv. Mater., 2012, 24:1987-1993 doi: 10.1002/adma.201200431

  2. [2]

     范乐庆, 李兆磊, 黄昀昉, 等.无机化学学报, 2015, 31(1):147-152 http://www.wjhxxb.cn/wjhxxbcn/ch/reader/view_abstract.aspx?flag=1&file_no=20150122&journal_id=wjhxxbcnFAN Le-Qing, LI Zhao-Lei, HUANG Yun-Fang, et al. Chinese J. Inorg. Chem., 2015, 31(1):147-152 http://www.wjhxxb.cn/wjhxxbcn/ch/reader/view_abstract.aspx?flag=1&file_no=20150122&journal_id=wjhxxbcn

  3. [3]

     Dong B, Liu D P, Wang X J, et al. Appl. Phys. Lett., 2007, 90:181117 doi: 10.1063/1.2735955

  4. [4]

     Sun L N, Peng H S, Stich M I J, et al. Chem. Commun., 2009:5000-5002

  5. [5]

     张俊文, 谭宁会, 刘应亮, 等.无机化学学报, 2010, 26(2):229-232 http://www.wjhxxb.cn/wjhxxbcn/ch/reader/view_abstract.aspx?flag=1&file_no=20100208&journal_id=wjhxxbcnZHANG Jun-Wen, TAN Ning-Hui, LIU Ying-Liang, et al. Chinese J. Inorg. Chem., 2010, 26(2):229-232 http://www.wjhxxb.cn/wjhxxbcn/ch/reader/view_abstract.aspx?flag=1&file_no=20100208&journal_id=wjhxxbcn

  6. [6]

     Cao B S, Wu J L, Feng Z Q, et al. Mater. Chem. Phys., 2013, 142:333-338 doi: 10.1016/j.matchemphys.2013.07.025

  7. [7]

     Chen C W, Lee P H, Chan Y C, et al. J. Mater. Chem. B, 2015, 3:8293-8302 doi: 10.1039/C5TB01393C

  8. [8]

     Wu X, Chen J Y, Shen J, et al. Bioconjugate Chem., 2015, 26: 166-175 doi: 10.1021/bc5003967

  9. [9]

     Yin Z, Zhu Y S, Xu W, et al. Chem. Commun., 2013, 49: 3781-3783 doi: 10.1039/c3cc40829a

  10. [10]

      Sun Y, Zhu X J, Peng J J, et al. ACS Nano, 2013, 7(12): 11290-11300 doi: 10.1021/nn405082y

  11. [11]

      吴金磊, 曹保胜, 冯志庆, 等.光学学报, 2014, 34:s116004 http://www.cnki.com.cn/Article/CJFDTOTAL-SYQY201603027.htmWU Jin-Lei, CAO Bao-Sheng, FENG Zhi-Qing, et al. Acta Optica Sinica, 2014, 34:s116004 http://www.cnki.com.cn/Article/CJFDTOTAL-SYQY201603027.htm

  12. [12]

      Li D D, Shao Q Y, Dong Y, et al. J. Phys. Chem. C, 2014, 118:22807-22813 doi: 10.1021/jp507804h

  13. [13]

      Li Z H, Park W, Zorzetto G, et al. J. Chem. Mater., 2014, 26:1770-1778 doi: 10.1021/cm4023425

  14. [14]

      Dong H, Sun L D, Yan C H. Chem. Soc. Rev., 2015, 44: 1608-1634 doi: 10.1039/C4CS00188E

  15. [15]

      Wang F, Han Y, Lim C S, et al. Nature, 2010, 463:1061-1065 doi: 10.1038/nature08777

  16. [16]

      Li Z P, Dong B, He Y Y, et al. J. Lumin, 2012, 132:1646-1648 doi: 10.1016/j.jlumin.2012.02.034

  17. [17]

      Xu W, Min X L, Chen X, et al. Sci. Rep., 2014, 4:5087

  18. [18]

      REN Lu-Quan(任露泉). Design of Experiment and Optimiz-ation(试验设计及其优化). Beijing: Science Press, 2009: 174-180

  19. [19]

      HE Wei(何为), XUE Wei-Dong(薛卫东), TANG Bin(唐斌). The Method of Optimal Design of Experiment and Data Analysis(优化试验设计方法及数据分析). Beijing: Chemical Industry Press, 2012: 191-194

  20. [20]

      翟梓会, 孙佳石, 张金苏, 等.物理学报, 2013, 62(20): 203301 doi: 10.7498/aps.62.203301ZHAI Zi-Hui, SUN Jia-Shi, ZHANG Jin-Su, et al. Acta Phys. Sin., 2013, 62(20): 203301 doi: 10.7498/aps.62.203301

  21. [21]

      Cao B S, He Y Y, Feng Z Q, et al. Sens. Actuators B, 2011, 159:8-11 doi: 10.1016/j.snb.2011.05.018

  22. [22]

      Pollnau M, Gamelin D R, Lüthi S R, et al. Phys. Rev. B, 2000, 61(5):3337-3346 doi: 10.1103/PhysRevB.61.3337

  23. [23]

      Zhou S Q, Li C R, Liu Z F, et al. Opt. Mater., 2007, 30(4): 513-516 doi: 10.1016/j.optmat.2007.01.005

  24. [24]

      Xiang S Y, Chen B J, Zhang J S, et al. Opt. Mater. Express, 2014, 4(9):1966-1980 doi: 10.1364/OME.4.001966

  25. [25]

      Tian Y, Hua R N, Chen B J, et al. CrystEngCommun, 2012, 14(23):8110-8116 doi: 10.1039/c2ce26101d

  26. [26]

      Liang Z Q, Zhang J S, Sun J S, et al. Physica B, 2013, 412: 36-40 doi: 10.1016/j.physb.2012.12.013

  27. [27]

      Tian B N, Chen B J, Tian Y, et al. J. Phys. Chem. Solids, 2012, 73:1314-1319 doi: 10.1016/j.jpcs.2012.06.016

• 

  图 1  (a) Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇纳米晶粉末的XRD图; (b)纳米晶粉末的主要衍射峰，插图为晶格常数和晶粒尺寸随Yb³⁺掺杂浓度的变化关系

  Figure 1  (a) XRD patterns of Er³⁺-Yb³⁺ co-doped Gd₂Ti₂O₇; (b) Main diffraction peaks of the powder

  Inset: the lattice constant and the grain size of Er³⁺-Yb³⁺ co-doped Gd₂Ti₂O₇ powder as a function of Yb ³⁺ concentration

  下载: 全尺寸图片 幻灯片
  

  图 2  Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇的上转换发光光谱

  Figure 2  Upconversion emission spectra of Er³⁺-Yb³⁺co-doped Gd₂Ti₂O₇

  下载: 全尺寸图片 幻灯片
  

  图 3  红光发光强度随Er³⁺/Yb³⁺共掺杂浓度变化图

  Figure 3  Dependence of red emission intensity on the Er³⁺/Yb³⁺ co-doped concentration

  下载: 全尺寸图片 幻灯片
  

  图 4  Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇上转换发光强度随泵浦激光功率的变化

  Figure 4  Log-log plots of upconversion emissions for Er³⁺-Yb³⁺ co-doped Gd₂Ti₂O₇ versus excitation power of pump laser

  下载: 全尺寸图片 幻灯片
  

  图 5  Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇的上转换发光能级图

  Figure 5  Schematic energy levels diagram of Er³⁺-Yb³⁺ co-doped Gd₂Ti₂O₇ powder

  下载: 全尺寸图片 幻灯片
  

  图 6  Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇最优样品的绿色上转换发光随温度的变化关系图

  Figure 6  Green upconversion emissions for Er³⁺-Yb³⁺ co-doped Gd₂Ti₂O₇ versus temperature

  下载: 全尺寸图片 幻灯片
  

  图 7  绿色上转换发光强度比R(I_H/I_S)与温度之间的函数关系图

  Figure 7  Green upconversion emissions ratio of R(I_H/I_S) as a function of temperature

  下载: 全尺寸图片 幻灯片
  

  图 8  Er³⁺-Yb³⁺共掺杂Gd₂Ti₂O₇最优样品的红色上转换发光随温度的变化关系图

  Figure 8  Red upconversion emissions for Er³⁺-Yb³⁺ co-doped Gd₂Ti₂O₇ versus temperature

  下载: 全尺寸图片 幻灯片

  表 1  均匀设计实验

  Table 1.  Uniform experimental design

  Number	Factor
  	Er3+x1 / %	Yb3+x2 / %	yred
  1	1(1.000)	4(34.125)	20 472.0
  2	2(2.000)	8(79.625)	811.2
  3	3(3.000)	3(22.750)	144 563.7
  4	4(4.000)	7(68.250)	1 590.3
  5	5(5.000)	2(11.375)	249 612.0
  6	6(6.000)	6(56.875)	3 638.5
  7	7(7.000)	1(0.000)	4 011.1
  8	8(8.000)	5(45.500)	5 487.8
  9	9(9.000)	9(91.000)	2 947.2

  下载: 导出CSV

  表 2  自然因素水平编码表

  Table 2.  Natural factors level code

  zj(xj)	z1(Er3+) / %	z2(Yb3+) / %
  z2j(r)	7	20
  z0j+Δj(1)	6.414	17.072
  z0j(0)	5	10
  z0j-Δj(-1)	3.586	2.928
  z1j(-r)	3	0
  Δj=(z2j-z1j)/(2r)	1.414	7.072
  xj=(zj-z0j)Δj	xj=(zj-5)/1.414	xj=(Zj-10)/7.072

  下载: 导出CSV

  表 3  二次通用旋转组合设计的实验方案与积分强度的结果表

  Table 3.  Integrated intensity and experiment scheme of quadratic general rotary unitized design

  Number	Factor
  	x0	x1	x2	x1x2	x12	x22	yred
  1	1	1	1	1	1	1	190 597.4
  2	1	1	-1	-1	1	1	77 864.2
  3	1	-1	1	-1	1	1	162 591.9
  4	1	-1	-1	1	1	1	42 600.0
  5	1	r	0	0	r2	0	171 357.2
  6	1	-r	0	0	r2	0	195 836.9
  7	1	0	r	0	0	r2	144 919.0
  8	1	0	-r	0	0	r2	4 406.6
  9	1	0	0	0	0	0	209 290.1
  10	1	0	0	0	0	0	193 202.4
  11	1	0	0	0	0	0	193 850.4
  12	1	0	0	0	0	0	181 725.9
  13	1	0	0	0	0	0	192 503.6

  下载: 导出CSV

  表 4  红光的T-检验及F-检验方差分析表

  Table 4.  T-test and F-test with analysis of variance of red light

  Source of variance	Sum of square of deviations	Degree of freedom	T statistics and F ratio	Significance level (α)	Significance
  x0	188 402 148 575.5	1	27.324	0.001	****
  x1	102 640 109.4	1	0.638	0.6	Insignificant
  x2	23 264 302 986.2	1	9.601	0.001	****
  x1x2	13 172 163.3	1	0.228	0.9	Insignificant
  x12	427 310 576.6	1	1.301	0.3	Insignificant
  x22	26 996 053 801.8	1	10.340	0.001	****
  0rthogonal	50 667 839 069.6	5	40.157	0.01	****
  Residual	1 766 450 041.9	7	—	—	—
  Fidelity of simulation	1 379 177 538.3	3	4.748	0.01	—
  Error	387 272 503.5	4	—	—	—
  Sum	52 434 289 111.4	12	—	—	—
  Note: **** very significant level (α≤0.01); *** significant level (α≤0.1); ** quiet significant level (α≤0.25)

  下载: 导出CSV
•