English

• 2010年，英国曼彻斯特大学的安德烈·海姆和康斯坦丁·诺沃肖洛夫教授被授予诺贝尔物理学奖，以表彰他们在二维石墨烯材料方面的开拓性研究，有关石墨烯的研究自此迅速风靡全球，世界上物理、化学、材料和电子等众多领域的学者都对其投入了巨大的研究热情^{[1, 2]}。石墨烯是指由六方蜂窝状晶格排列的一个原子层厚的碳原子结构，它是构成零维的富勒烯、一维的碳纳米管和三维的石墨等其他碳材料的基本结构单元^{[3, 4]}。石墨烯独特的二元化电子价键结构决定了其丰富而独特的力学、电学和光学性质。石墨烯具有高杨氏模量 (1Tpa)，是钢铁的200倍；高热导率 (5000W ·m^-1 ·K^-1)，是金刚石的3倍；高本征载流子迁移率 (2000cm² ·V^-1 ·s^-1)，是商用硅的10倍；高表面积 (2639m² g^-1)、高光学透过率 (97.7%) 以及室温下半整数的量子霍尔效应等性能^[5~8]，预示着其在纳米器件、场效应晶体管、高性能电池和超级电容器、自旋器件、透明导电电极、机电共振器、太阳能电池、复合材料以及储氢材料等诸多领域都具有良好的应用前景^[9~13]。

  拉曼光谱作为一种灵敏、便捷的技术，已被成功地用于表征石墨烯的结构和特性。研究表明，通过对拉曼光谱2D峰的峰值、半峰宽变化程度的确定，可以准确地判断石墨烯的层数^[14]；拉曼光谱G峰强度随石墨烯层数增加而增加，二者具有高度线性关系^[15]。同时，研究者发现G峰和2D峰的峰值及半峰宽的变化情况还与石墨烯的堆垛顺序息息相关^{[16, 17]}。石墨烯的边缘手性可以通过D峰与G峰的峰值与强度变化情况来判断^{[18, 19]}。

  迄今为止，拉曼光谱多局限于研究Si/SiO₂标准衬底上的纯石墨烯。未来对石墨烯独特属性与其在电子材料中应用的需求，要求将石墨烯沉积在不同的基底上或用各种不同的材料对石墨烯进行掺杂。本文对沉积在不同基底上及不同掺杂的石墨烯的拉曼光谱研究做一简单总结。

  1   拉曼光谱在石墨烯沉积基底方面的研究

  石墨烯是只有一个原子层厚的碳原子层，在最初研究中尚不清楚石墨烯与沉积基底之间是否会有一些强烈的交互作用，这些交互作用是否会引起石墨烯与基底之间的耦合、石墨烯表面缺陷甚至两种表面的电荷缺失，最终是否会导致石墨烯拉曼光谱发生变化。研究者通过对沉积在不同基底上的石墨烯的拉曼光谱的观察，分析了基底对拉曼光谱的影响。

  图 1为沉积在Si/SiO₂标准衬底上采用514nm波长激光激发时的单层石墨烯与石墨的典型拉曼光谱^[20]。图中显示了石墨烯的主要特征峰：产生于石墨烯第一布里渊区二级双共振过程的2D峰 (位于2700cm^-1附近)^[21]、产生于第一布里渊区面内纵向声子模与横向声子模结合的D′峰 (位于2450cm^-1附近) 和产生于第一布里渊区一级拉曼散射过程的G峰 (位于1580cm^-1附近)^{[22, 23]}。在实际应用中，要根据石墨烯的应用方向选择不同的基底，例如，光学电子器件就需要蓝宝石、单晶石英或玻璃等透明的基底来沉积石墨烯。对不同基底上的石墨烯进行拉曼测试时，拉曼特征峰的峰值易受基底的影响向低频或高频方向位移。

  图 1  沉积在Si/SiO₂标准衬底上的单层石墨烯和石墨的拉曼光谱^[20] Figure 1.  Raman spectra of single layer graphene and graphite on Si/SiO₂ substrate ^[20]

  图选项

  下载全尺寸图像

  下载幻灯片

  图 2为沉积在铟锡氧化物 (ITO) 基底上的单层石墨烯的拉曼光谱^[24]。与Si/SiO₂标准衬底上拉曼光谱相比，G峰和2D峰分别向低频方向位移了6cm^-1和20cm^-1。G峰与2D峰红移的原因目前还尚不明确，但是特征峰频率的降低意味着沉积在ITO基底上的石墨烯层的晶胞常数扩大了。

  图 2  沉积在ITO基底上的单层石墨烯拉曼光谱^[24] Figure 2.  Raman spectrum of single layer graphene on ITO substrate ^[24]

  图选项

  下载全尺寸图像

  下载幻灯片

  图 3为沉积在蓝宝石 (11-20) 晶面上的单层石墨烯的拉曼光谱，从图中可以看出，拉曼G峰向低频方向位移了约5cm^-1[25]。同时，相关研究表明，在蓝宝石 (0001) 和 (1-102) 晶面上，单层石墨烯的G峰较 (11-20) 晶面向高频方向有不同程度的位移。这是由于蓝宝石不同晶面上的水分子密度不同，水层与石墨烯相互作用的差异引起其G峰蓝移程度的不同^[26]。

  图 3  沉积在蓝宝石基底上的单层石墨烯的拉曼光谱^[25] Figure 3.  Raman G peak of single layer graphene on sapphire substrate ^[25]

  图选项

  下载全尺寸图像

  下载幻灯片

  图 4为沉积在玻璃基底上的单层石墨烯的拉曼光谱^[27]。拉曼G峰的位置与Si/SiO₂标准衬底上的接近，在某些情况下，拉曼G峰可能会发生分裂，但平均峰值仍在1580cm^-1处。玻璃表面随机分布的杂质或表面电荷的作用可以解释光谱中的分裂现象^[28]。因为玻璃是无定形的，测试中激光照射引入了额外的振动模式，导致谱图中出现了没有预计到的杂峰。

  图 4  沉积在玻璃基底上的单层石墨烯拉曼光谱^[27] Figure 4.  Raman spectrum of single layer graphene on glass substrate ^[27]

  图选项

  下载全尺寸图像

  下载幻灯片

  图 5为沉积在玻璃基底上的双层石墨烯的拉曼光谱。在光谱中4个子峰仍存在，这遵循了石墨烯的二级双共振模式^[29]。

  图 5  沉积在玻璃基底上的双层石墨烯拉曼光谱^[29] Figure 5.  Raman spectrum of bilayer graphene on glass substrate ^[29]

  图选项

  下载全尺寸图像

  下载幻灯片

  基于这些研究可以确定，2D峰用于判断石墨烯层数这一结论在不同的基底上同样适用，甚至是含有大量缺陷且无定形的玻璃基底。

  2   拉曼光谱在石墨烯掺杂方面的研究

  由于石墨烯的价带和导带相交于狄拉克点并呈线性色散关系，所以石墨烯是一种零带隙的半导体材料^[30]。零带隙结构使石墨烯电子器件开关比低，且漏电流大。通过掺杂可以有效地打开石墨烯的带隙，这是其应用于电子信息器件的必要条件，而拉曼光谱是检测掺杂效应的理想工具。

  2.1   拉曼光谱在石墨烯电化学掺杂方面的研究

  电化学掺杂是以电极为介质，提供 (n型掺杂) 或者接收 (p型掺杂) 电子，作为氧化或还原手段，从而改变共轭聚合物的荷电状态，达到提高其导电能力的目的。电化学掺杂没有实质性物质参与，因而不影响共轭聚合物的化学组成，掺杂方法简便，且掺杂过程具有可逆性与可控性。本节主要介绍施加门电压对石墨烯拉曼光谱的影响。

  外电场可使石墨烯的费米能级从狄拉克点处发生上移或下移，从而使本征载流子变成电子型或空穴型，进而使石墨烯表现出n型掺杂与p型掺杂的特性^[31]。

  图 6为在石墨烯表面施加垂直电场的情况下，石墨烯拉曼光谱G峰与2D峰随电场强度变化的情况^[32]。显然，拉曼峰值与半峰宽都受到了门电压的影响，且G峰较2D峰的变化情况更加明显。从图 7中更能明确地观察到^{[33, 34]}，单层石墨烯的拉曼G峰半峰宽在n型掺杂与p型掺杂时都发生了缩减，且G峰在n型掺杂与p型掺杂时都向高频方向位移，n型掺杂时位移了约25cm^-1，p型掺杂时位移了约30cm^-1，而2D峰在n型掺杂时向低频方向位移，p型掺杂时向高频方向位移。因此，可以通过石墨烯拉曼光谱的变化定性电场效应下的掺杂类别并定量石墨烯的载流子浓度。

  图 6  石墨烯的 (a) G峰和 (b)2D峰随门电压变化的关系^[32] Figure 6.  Evolution of the (a) G band and (b) 2D band of the monolayer graphene with gate voltage ^[32]

  图选项

  下载全尺寸图像

  下载幻灯片

  图 7  (a) G峰半峰宽与电子掺杂、空穴掺杂浓度变化的关系 (黑点为测量值，蓝线为理论值) ^[33]；(b) G峰峰值随电子掺杂、空穴掺杂浓度变化的关系 (黑线为绝热条件下测得，蓝线为不绝热条件下测得) ^[34] Figure 7.  (a) FWHM (G) as a function of hole and electron doping (the black circles are measured value, the blue line are theoretical value) ^[33]; (b) the frequency of G band as a function of electron and hole doping (the black lines are measured under adiabatic condition, the blue lines are measured under non-adiabatic condition) ^[34]

  图选项

  下载全尺寸图像

  下载幻灯片

  除了以上结论，还可以通过石墨烯G峰峰值定量其与费米能级|EF|之间的关系^[33]：

  其中α′=4.39×10^-3， < D_Γ²>_F=45.6eV²Å^-2是E_2g振动模的形变势能，∈_F是费米能级的改变量，M是碳原子的质量，ω₀是未掺杂石墨烯拉曼G峰的峰值，v_F是石墨烯的费米加速度。因此，可以通过对石墨烯的拉曼光谱谱峰变化情况的分析来定量电场掺杂效应下石墨烯费米能级的变化。

  2.2   拉曼光谱在石墨烯化学掺杂方面的研究

  化学掺杂是利用氧化还原试剂直接与聚合物进行氧化还原反应，改变聚合物的简电状态。图 8比较了纯石墨烯 (HG)、B/C=1.2%的掺杂石墨烯 (BG1)、B/C=3.1%的掺杂石墨烯 (BG2) 和N/C=0.6%的掺杂石墨烯 (NG) 在632.8nm波长激光激发下的拉曼光谱^[35]。在1000~3000 cm^-1区域内显示了3个主要的特征峰：G峰 (~1570cm^-1)、D峰 (~1320cm^-1) 和2D峰 (~2640cm^-1)。值得注意的是，G峰在B掺杂与N掺杂的情况下都向高频方向发生了位移，这与电化学掺杂中的现象类似，而BG2样品的拉曼G峰向高频方向的位移程度较BG1样品更大，NG样品中的拉曼G峰向高频方向的位移程度最小^[36]。

  图 8  纯石墨烯 (HG) 和掺杂石墨烯 (BG和NG) 的拉曼光谱^[35] Figure 8.  Raman spectra of undoped (HG) and doped (BG和NG) graphenes ^[35]

  图选项

  下载全尺寸图像

  下载幻灯片

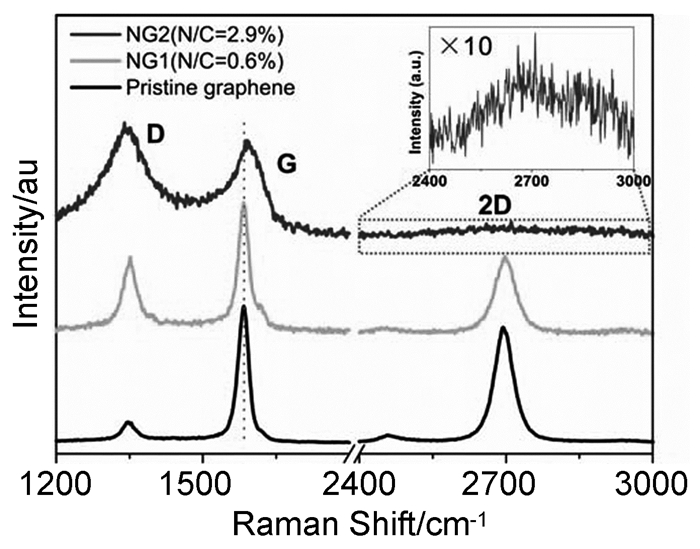
  图 9比较了纯石墨烯、N/C=0.6%的掺杂石墨烯 (NG1) 和N/C=2.9%的掺杂石墨烯 (NG2) 的拉曼光谱^[37]。从图中可以看出，NG2样品中的拉曼G峰向高频方向的位移程度较NG1样品更大一些，表明掺杂物质的含量会影响G峰的位移程度。从两图中都可以发现，在所有的掺杂样品中D峰强度呈升高趋势，这是因为掺杂剂的加入使缺陷浓度增加。同时，G峰强度随科恩异常效应 (Kohn anomaly) 的减弱呈减小趋势，且D峰强度要高于G峰强度，而石墨烯第一布里渊区非等价K点附近声子频率的减弱使2D峰的强度呈减小趋势，与G峰强度类似。从以上结论看出，B掺杂与N掺杂石墨烯可以表现出p型掺杂与n型掺杂属性^[38]。可以通过系统调节B和N的掺杂浓度来调控掺杂程度，而通过拉曼光谱可以判断石墨烯的掺杂水平^[34]。

  图 9  未掺杂及低浓度和高浓度氮掺杂的石墨烯的拉曼光谱^[37] Figure 9.  Raman spectra of original graphene and low concentration and high concentration of nitrogen doped graphene ^[37]

  图选项

  下载全尺寸图像

  下载幻灯片

  研究表明，掺杂石墨烯与未掺杂石墨烯样品的晶粒尺寸遵循如下关系^[39]：

  其中，λ表示拉曼测试的激发光源的波长，I_D、I_G表示D峰与G峰的强度。HG、BG1、BG2和NG样品的晶粒尺寸分别为64、30、26和43 nm，表明掺杂石墨烯样品的晶粒尺寸要小于未掺杂的样品。同时发现，随着掺杂B含量的增加，晶粒尺寸呈减小的趋势，而掺杂量最小的NG样品的晶粒尺寸比掺杂量最大的BG2样品的要大。其中的差异与它们的结构有关：B—C键比C—C键的键长约长0.5%，而N—C键与C—C键的键长相似，B掺杂石墨烯晶格常数发生变化，但是晶格的变化是高度不对称的，使石墨烯声子振动频率大幅降低，最终导致晶粒尺寸的减小。相关研究表明BG和NG样本的电阻率比无掺杂石墨烯要低得多^[40]。

  3   结语

  本文主要介绍了沉积在不同基底上与不同掺杂石墨烯的拉曼光谱的研究。在不同基底上，石墨烯拉曼光谱的谱峰发生了不同程度的位移，半峰宽也有不同程度的变化。电化学掺杂与化学掺杂总的来说表现为n型掺杂与p型掺杂的属性，通过对石墨烯拉曼光谱变化情况的分析可以检测石墨烯的掺杂类别与掺杂程度。将石墨烯沉积在不同的基底上或用各种不同材料对石墨烯进行掺杂，对石墨烯在电子器件材料中的应用至关重要。目前，我国在这方面的研究还存在许多科学与技术上的问题，相信通过广大学者坚持不懈的研究与探索，这些难题会逐个被解决，终将使石墨烯广泛应用于工业生产中。

• 1. [1]

     K S Novoselov, A K Geim, S V Morozov et al. Science, 2004, 306(5696):666-669. doi: 10.1126/science.1102896

  2. [2]

     K S Novoselov, D Jiang, F Schedinet al. PNAS, 2005, 102(30):10451-0453. doi: 10.1073/pnas.0502848102

  3. [3]

     J C Meyer, A K Geim, M I Katsnelson et al. Nature, 2007, 446(7131):60-63. doi: 10.1038/nature05545

  4. [4]

     K S Novoselov. Nat. Mater., 2007, 6(3):183-191. doi: 10.1038/nmat1849

  5. [5]

     C Lee, X Wei, J W Kysar et al. Science, 2008, 321(5887):385-388. doi: 10.1126/science.1157996

  6. [6]

     J S Bunch, S S Verbridge, J S Alden et al. Nano Lett., 2008, 8(8):2458-2462. doi: 10.1021/nl801457b

  7. [7]

     Y Zhang, Y W Tan, H L Stormer et al. Nature, 2005, 438(7065):1-7.

  8. [8]

     D Shin, S K Bae, C Yan et al. Carbon Lett., 2012, 13(1):1-16. doi: 10.5714/CL.2012.13.1.001

  9. [9]

     X Wang, L Zhi, K Müllen. Nano Lett., 2008, 8(1):323-327. doi: 10.1021/nl072838r

  10. [10]

      H Yang, J Heo, S Park et al. Science, 2012, 336(6085):1140-1143. doi: 10.1126/science.1220527

  11. [11]

      M D Stoller, S Park, Y Zhu et al. Nano Lett., 2008, 8(10):3498-3502. doi: 10.1021/nl802558y

  12. [12]

      V C Tung, L M Chen, M J Allen et al. Nano Lett., 2009, 9(5):1949-1955. doi: 10.1021/nl9001525

  13. [13]

      X Yan, X Cui, B Li et al. Nano Lett., 2010, 10(5):1869-1873. doi: 10.1021/nl101060h

  14. [14]

      A C Ferrari. Solid State Commun., 2007, 143(1-2):47-57. doi: 10.1016/j.ssc.2007.03.052

  15. [15]

      A Gupta, G Chen, P Joshi et al. Nano Lett., 2006, 6(12):2667-2673. doi: 10.1021/nl061420a

  16. [16]

      C H Lui, Z Li, Z Chen et al. Nano Lett., 2011, 11(1):164-69. doi: 10.1021/nl1032827

  17. [17]

      C Cong, T Yu, K Sato et al. ACS Nano, 2011, 5(11):8760-768. doi: 10.1021/nn203472f

  18. [18]

      X Zhang, Q Q Li, W P Han et al. Nanoscale, 2014, 6(13):7519-7525. doi: 10.1039/c4nr00499j

  19. [19]

      M Begliarbekov, O Sul, S Kalliakos et al. Appl. Phys. Lett., 2010, 97(3):031908. doi: 10.1063/1.3464972

  20. [20]

      A C Ferrari, J C Meyer, V Scardaci et al. Phys. Rev. Lett., 2006, 97(18):13831-13840. http://med.wanfangdata.com.cn/Paper/Detail/PeriodicalPaper_PM17155573

  21. [21]

      C Thomsen, S Reich. Phys. Rev. Lett., 2001, 85(24):5214-5217.

  22. [22]

      S García, A Marín. Phys. Rev. B, 2007, 76(76):4692-4692.

  23. [23]

      F Tuinstra, J L Koenig. J. Chem. Phys., 1970, 53(3):1126-1130. doi: 10.1063/1.1674108

  24. [24]

      A Das, B Chakraborty, A K Sood. Bull. Mater. Sci., 2007, 31(3):579-584. doi: 10.1007/s12034-008-0090-5

  25. [25]

      I Calizo, S Ghosh, W Z Bao et al. Solid State Commun., 2009, 149(27-28):1132-1135. doi: 10.1016/j.ssc.2009.01.036

  26. [26]

      H Komurasaki, T Tsukamoto, K Yamazaki et al. J. Phys. Chem. C, 2012, 116(18):10084-10089. doi: 10.1021/jp301402u

  27. [27]

      I Calizo, S Ghosh, D Teweldebrhan et al. Raman nanometrology of graphene on arbitrary substrates and at variable temperature//Nano Science+Engineering. Internat-ional Society for Optics and Photonics, 2008:70371B.

  28. [28]

      I Calizo, W Z Bao, F Miao et al. Appl. Phys. Lett., 2007, 91(20):201904. doi: 10.1063/1.2805024

  29. [29]

      I Calizo, D Teweldebrhan, W Z Bao et al. J. Phys. Conf. Ser., 2008,109:012008. doi: 10.1088/1742-6596/109/1/012008

  30. [30]

      K S Novoselov, A K Geim, S V Morozov et al. Nature, 2005, 438(7065):197-200. doi: 10.1038/nature04233

  31. [31]

      张芸秋, 梁勇明, 周建新. 化学学报, 2014, 72(3):367-377. http://www.cnki.com.cn/Article/CJFDTotal-HXXB201403009.htm

  32. [32]

      J Yan, Y Zhang, P Kim et al. Phys. Rev. Lett., 2007, 98(16):166802. doi: 10.1103/PhysRevLett.98.166802

  33. [33]

      S Pisana, M Lazzeri, C Casiraghi et al. Nat. Mater., 2007, 6(3):198-201. doi: 10.1038/nmat1846

  34. [34]

      A Das, S Pisana, B Chakraborty et al. Nat. Nanotech., 2008, 3(4):210-215. doi: 10.1038/nnano.2008.67

  35. [35]

      L S Panchakarla, K S Subrahmanyam, S K Saha et al. Adv. Mater., 2009, 21(46):4726-4730.

  36. [36]

      A Das, A K Sood, A Govindaraj et al. Phys. Rev. Lett., 2007, 99(13):136803-136803. doi: 10.1103/PhysRevLett.99.136803

  37. [37]

      C Zhang, L Fu, N Liu et al. Adv. Mater., 2011, 23(8):1020-1024. doi: 10.1002/adma.201004110

  38. [38]

      X Li, L Fan, Z Li et al. Adv. Energy Mater., 2012, 2(4):425-429. doi: 10.1002/aenm.201100671

  39. [39]

      L G Cancado, K Takai, T Enoki et al. Appl. Phys. Lett., 2006, 88(16):163106. doi: 10.1063/1.2196057

  40. [40]

      R Voggu, B Das, C S Rout et al. J. Phys. Condens. Matter, 2008, 20(47):1005-1008.

• 

  图 1  沉积在Si/SiO₂标准衬底上的单层石墨烯和石墨的拉曼光谱^[20]

  Figure 1  Raman spectra of single layer graphene and graphite on Si/SiO₂ substrate ^[20]

  下载: 全尺寸图片 幻灯片
  

  图 2  沉积在ITO基底上的单层石墨烯拉曼光谱^[24]

  Figure 2  Raman spectrum of single layer graphene on ITO substrate ^[24]

  下载: 全尺寸图片 幻灯片
  

  图 3  沉积在蓝宝石基底上的单层石墨烯的拉曼光谱^[25]

  Figure 3  Raman G peak of single layer graphene on sapphire substrate ^[25]

  下载: 全尺寸图片 幻灯片
  

  图 4  沉积在玻璃基底上的单层石墨烯拉曼光谱^[27]

  Figure 4  Raman spectrum of single layer graphene on glass substrate ^[27]

  下载: 全尺寸图片 幻灯片
  

  图 5  沉积在玻璃基底上的双层石墨烯拉曼光谱^[29]

  Figure 5  Raman spectrum of bilayer graphene on glass substrate ^[29]

  下载: 全尺寸图片 幻灯片
  

  图 6  石墨烯的 (a) G峰和 (b)2D峰随门电压变化的关系^[32]

  Figure 6  Evolution of the (a) G band and (b) 2D band of the monolayer graphene with gate voltage ^[32]

  下载: 全尺寸图片 幻灯片
  

  图 7  (a) G峰半峰宽与电子掺杂、空穴掺杂浓度变化的关系 (黑点为测量值，蓝线为理论值) ^[33]；(b) G峰峰值随电子掺杂、空穴掺杂浓度变化的关系 (黑线为绝热条件下测得，蓝线为不绝热条件下测得) ^[34]

  Figure 7  (a) FWHM (G) as a function of hole and electron doping (the black circles are measured value, the blue line are theoretical value) ^[33]; (b) the frequency of G band as a function of electron and hole doping (the black lines are measured under adiabatic condition, the blue lines are measured under non-adiabatic condition) ^[34]

  下载: 全尺寸图片 幻灯片
  

  图 8  纯石墨烯 (HG) 和掺杂石墨烯 (BG和NG) 的拉曼光谱^[35]

  Figure 8  Raman spectra of undoped (HG) and doped (BG和NG) graphenes ^[35]

  下载: 全尺寸图片 幻灯片
  

  图 9  未掺杂及低浓度和高浓度氮掺杂的石墨烯的拉曼光谱^[37]

  Figure 9  Raman spectra of original graphene and low concentration and high concentration of nitrogen doped graphene ^[37]

  下载: 全尺寸图片 幻灯片
•