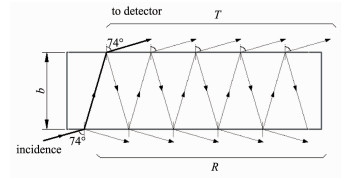
 Figure Scheme 1.
Scheme of the MTR-IR optical path
Figure Scheme 1.
Scheme of the MTR-IR optical path

多次透射反射红外光谱法灵敏和准确地测量单晶硅中间隙氧和代位碳的含量
English
Sensitive and Accurate Measurement of Interstitial Oxygen and Substitutional Carbon in Single Crystalline Silicon by Multiple Transmission-Reflection Infrared Spectroscopy (MTR-IR)
-
0 Introduction
Silicon-based semiconductor industry, as a miracle in the human beings history, continues to develop at considerably high growth rates already for half a century. Recently, solar energy has been recognized in common as an alternative sustainable energy source due to the increased awareness of the global energy crisis [1]. Silicon solar cells have become the most important photovoltaic products owing to the sophisticated manufacturing technology and the reliable cell quality. The quality control of silicon materials is crucial to both semiconductor and solar cell industries of silicon. During the Czochralski (CZ) procedure in growing silicon single crystals for semiconductor and photovoltaic industry, oxygen and carbon are incorporated into the molten silicon to different extents from the quartz crucibles and the graphite heaters. As oxygen atoms can find sites within the lattice structure among silicon atoms, interstitial oxygen (Oi) appears. Moreover, carbon atoms occupy positions generally taken by silicon atoms in the lattice structure, and this kind of impurity is defined as substitutional carbon (Cs)[1-3].
Interstitial oxygen and substitutional carbon are the main forms of oxygen and carbon impurities existing in silicon. Their different levels cause different physical and electrical effects in silicon, which have been extensively investigated and correlated[4-6]. Although Oi in suitable concentrations possesses an advantage to enhance the mechanical strength of silicon because of its nailing for stretching of dislocation in the silicon lattice, higher concentrations will result in electrically active defects that decrease the performance of the devices. Thus a gettering technique has been developed to decrease Oi and avoid defects during the silicon crystal growth procedure. High content of Cs affects the way Oi nucleates and precipitates, as well as resulting in softening and breakdown of electronic components[7-10]. Consequently, to control the silicon quality for high performance devices, it is absolutely necessary to monitor the content of Oi and Cs in silicon wafers more accurately and sensitively.
Various techniques have been applied to determine the content of Oi and Cs in bulk silicon. These techniques consist of gas fusion analysis, secondary ion mass spectrometry, charged particle activation analysis and neutron activation analysis etc., all of which are destructive, costly and time consuming[1]. In addition, the above methods measure the total content of elemental oxygen and carbon, including Oi and Cs and other forms of oxygen and carbon. Thus they are not specific for measuring the concentration of Oi (atoms per cm3, abbreviated as cOi, cm-3) and of Cs (atoms per cm3, abbreviated as cCs, cm-3). By contrast, infrared analysis is specific to cOi and cCs in silicon. Silicon atoms form bonds with the adjacent oxygen atoms (Si-O-Si) and carbon atoms (Si-C) in the lattice structure [11-13]. The interstitial oxygen is in the form of Si-O-Si, giving three vibration peaks centered at 1 107 cm-1 (strong), 513 cm-1 (medium) and 1 718 cm-1 (weak) respectively. Among the three bands, the strongest one at 1 107 cm-1 is usually used to determine cOi[14-16]. The substitutional carbon in the form of Si-C gives a vibration band at 605 cm-1. However the Si-C band overlaps with the strong silicon lattice vibration (Si-Si) at 605 cm-1, which renders the measurement of cCs delicate. The amount of light absorbed by Si-O-Si and Si-C is proportional to the concentration of atoms forming the bonds. Thus their corresponding infrared bands are measured and manipulated to quantitate cOi and cCs respectively. The calculation procedure is composed of subtraction of a reference (free of Oi and Cs) absorption band from a samples band, and subsequently calculation of cOi and cCs using the following formulae generally.
A=αb α=εc
where A is the measured absorbance; ε is the absorption coefficient of a particular bond, cm2; b is the thickness of the sample, cm; c is the concentration of the impurity, cm-3.
The IR method for the levels of Oi and Cs can be carried out at ambient or low temperature. Although the latter is more accurate than the former, it is costly and time consuming to handle the measurement at the cryogenic temperature. Furthermore, the reflection loss of infrared light at both cryostat windows outweighs its advantages[17-20].
The room temperature IR method for cOi and cCs measurements is most commonly used in industry because it is easy and simple to operate. Generally the presently accepted standard method used in industry for cOi and cCs measurements is restricted to a silicon slice with a thickness of 2 mm and a diameter of the infrared beam by a one-time perpendicular transmission of the infrared beam (we name it “conventional IR”). The detection limits of cOi and cCs for a 2.0 mm thick single crystalline silicon are 1×1016 and 5×1015 cm-3 respectively[21-22]. The above quantitative analysis meets challenges in practice such as: 1) measurement errors become larger when cOi and cCs reach their own detection limits, 2) interference fringes from thin wafers below 0.3 mm thickness interfere the target band signal, 3) the single transmission measurement approach in a spot provides a localized spectrum with poor specimen statistics, compared to the multi-spot data collection in MTR-IR. Our newly developed MTR-IR (Scheme 1) provides an excellent quantitative approach for analysis of cOi and cCs, due to its up to one order of magnitude enhancement of infrared absorption signals on the same silicon slice from the conventional IR measurement[23-26]. In this letter, we applied the MTR-IR spectroscopy in analysis of cOi and cCs of 0.45 mm thick silicon wafers. Our MTR-IR method greatly improves the measurement sensitivity and accuracy, for example, reaching detection limits of cOi at 1×1015 cm-3 and cCs at 5×1014 cm-3 for the standard silicon specimens with a 2.0 mm thickness, which is one order of a magnitude lower than from the standard method. MTR-IR also attenuates the interference fringes of thin wafers greatly, and advances the representativeness of data collections.
1 Experimental
1.1 Substrates
Double-side-polished and〈100〉 oriented n-type silicon wafers (B doped, resistivity of 15 Ω·cm (CZ) and 3 000 Ω·cm (FZ) respectively, 0.45 mm thick, from Shanghai Junhe Electronic Materials Co. Ltd., China) were cut into rectangular shapes (16 mm×50 mm) for infrared analysis. CZ silicon wafers were used as samples and FZ as reference to measure the impurity concentrations of Oi and Cs respectively.
1.2 Wafer cleaning
Silicon wafers were cleaned with “piranha solution” (concentrated H2SO4/30%H2O2, 3:1, V/V) for 4 h (caution: piranha solution reacts violently with organic materials and should be handled with great care) to remove organic pollutants, followed by boiling in the mixture of NH3·H2O/H2O/H2O2 (1:1:1, V:V:V) for 30 min, then cooling to room temperature, rinsing with water, and storing in water. Silicon samples were immersed in 1% HF for 5 min to eliminate the native passivation silicon oxide layer, and dried with a stream of nitrogen just before the measurement.
1.3 Measurement
The optical setup was designed to adapt to any commercial FTIR spectrometers, which is Bruker 80v FTIR, in our case. MTR accessory with a Brewster incident angle of 74° was used. Unless specified, a DTGS detector and scan times of 100 at 4 cm-1 resolution were used for measurement over the wavenumber range from 400 to 4 000 cm-1.
The silicon sample was inserted between the two Au mirrors, with one end of the silicon slice protruding about 5 mm out of the incident spot, in order to make sure that the first incidence shot was on the silicon surface. The two guiding mirrors can be moved back and forth to get the maximal luminous flux in the DTGS detector. The incident angle was controlled at 74° by a micro-adjuster with a minimal angle scale of 0.225.
The whole measurement procedure was performed according to ASTM F 1188 and ASTM F 1391[21-22, 30]. Eight random samples from different batches were used. Each sample was measured successively 4 times by MTR and IR by slightly relocating the Si wafer each time in order to measure different sampling points. Therefore for each sample, 4 different sampling points were measured by IR, whereas 40 different sampling points measured by MTR-IR if N equals 10.
1.4 Theory/calculation
1.4.2 Theory of signal enhancement of MTR-IR
Presently, the conventional IR method for measurement of cOi and cCs is to place a 2 mm thick single crystalline silicon slice normally (or within the margin of error of a slightly oblique angle ≤10°) in the light path. The sampling length equals to the thickness of the slice. The illuminated area is a circle with a diameter of the light spot, so the resulting cOi and cCs just represent the impurities within a cylinder with a diameter of the light spot (depending on the aperture) and a height of 2 mm. Whereas in the MTR-IR setup, the infrared light reflects back and forth many times between two gold mirrors and simultaneously passes through the sampling silicon slice repeatedly and takes away the information of Oi and Cs by the resonance of Si-O-Si and Si-C bonds. So, the optical path is N(1+1/n2)1/2 times of the thickness of a silicon wafer (b), and correspondingly the absorbance is amplified N(1+1/n2)1/2 times[29].
At the Brewster angle of 74, when Rp=0, Rs=0.70, RAu=1, the phase change of p polarization light ψ=π, the following formula can be deduced from Eq.(1) and (4).
From Eq.(6), the sampling length is enlarged N(1+1/n2)1/2 times, assuming the recorded infrared spectral signal comes from the main optical path illustrated in Scheme 1, and all other infrared signals are ignored. The infrared light passes through a silicon slice N times in different regions, thus the collected signal is an integrated one of the whole optical path, physically and statistically representing Oi and Cs in the silicon slice better.
1.4.1 Comparison of computation models for conventional IR and MTR-IR
1.4.1.3 MTR method[27]
The light path of the computation model for MTR-IR refers to Scheme 1. Comparing Scheme 1 to Fig. 2, we observed that two gold mirrors enforce the light transmit through the silicon slice N times and simultaneously taking away the message of oxygen and carbon of the silicon sample. The optical path in the MTR-IR setup of Scheme 1 is N times of bB at the Brewster incidence. For simplicity, only the main light path is drawn in Scheme 1 with N=6, all other light paths by multiple reflections in the MTR setup are ignored. The transmittance for MTR-IR (TMTR) is deduced as follows (See supporting information for details of derivation of the formula of MTR-IR):
where TMTR is the transmittance of MTR, %;RAu is the reflectivity of gold; bMTR is the optical path through a silicon sample in the MTR-IR measurement, cm.
1.4.1.2 Brewster angle single incidence
The expression of TB for the single Brewster incidence refers to Eq.(3)[29].
where TB is the transmittance of the Brewster angle single transmission, %; Rs and Rp indicate the reflectance of s-and p-polarization respectively; the first (Rp=0) and the second term (Rs has a value) in the formula represent transmittance energy of p-polarization and s-polarization respectively, because the total transmittance energy equals the sum of p-polarization and s-polarization (p-or s-polarization holds 1/2 of the original light energy); the phase change introduced by the interfering multiple reflections on the boundaries of a silicon is considered.
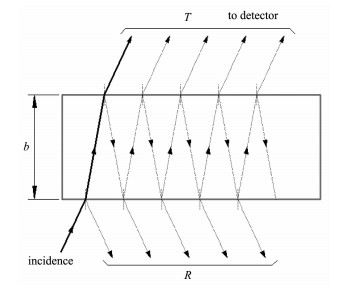
1.4.1.1 Conventional IR method
In the conventional IR method, the normal incident light passes a Si wafer (for convenience, a slightly oblique incidence is drawn in Fig. 1), the transmittance can be expressed as in Eq.(1) and (2)[21-22].
where T is the transmittance of normal incidence, %; R is reflectivity; n is refractive index; σ is wavenumber, cm-1; ψ is the phase change due to the interfering multiple reflections on the boundaries of the sample.
2 Results and discussion
2.1 Comparison of infrared traces between the conventional IR method and the MTR-IR method
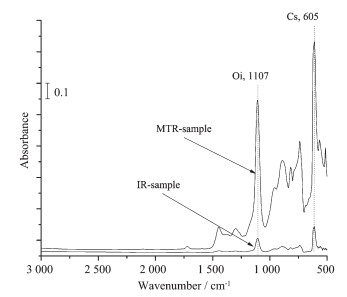
We listed two spectral traces of the same sample in Fig. 3, where the upper trace was obtained from MTR-IR and the lower trace from the conventional IR. All bands bear the same shape but their absorbance strength in MTR-IR is much higher than from IR, especially for the two strongest bands of Oi at 1 107 cm-1 and Cs at 605 cm-1. From the view point of quantitation, the bigger the absorbance value, the less the measurement error of Oi and Cs. Consequently cOi and cCs are more accurate and will have a lower detection limit. Because the absorption of Cs at 605 cm-1 overlaps with the strongest absorption of the silicon lattice vibration (Si-Si) centered at 610 cm-1, a FZ silicon reference is needed to subtract the silicon lattice vibration. Further, the real advantage of MTR-IR over the conventional IR not only lies in its ability to measure the spectra of Oi and Cs with stronger signals, but also with more sampling points for robust and representative measurements.
In Fig. 3, the peak height ratios of Oi and Cs (MTR-sample/IR-sample) were measured to be ~10 and ~8 respectively. Generally speaking, cCs is more difficult to be measured than cOi using the conventional IR method, due to two factors: (1) It is very tough to extract the much smaller Si-C peak from the strong Si-Si lattice band and therefore artificial results are often derived individually, thus an accurate quantitation is nearly impossible. (2) The Cs level in single crystalline silicon is always an order of magnitude lower than that of Oi. Judged from the signal enhancement, it is possible to extend the limit of detection of cOi at 1×1016 to 1×1015 cm-3 and cCs at 5×1015 to 5×1014 cm-3 for a 2.0 mm thick single crystalline silicon.
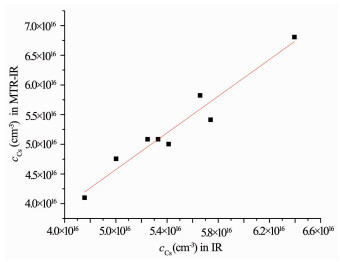
We randomly chose 8 samples to measure their cOi and cCs, both by the conventional IR and the MTR-IR methods, for verification of the MTR-IR method by the correlation curve in Fig. 4a and 4b (calculation details please see Supporting Information: 2. Data calculation). As it can be seen in Fig. 4a and 4b, both cOi and cCs are linearly correlated. The linear relationship of both cOi and cCs proved the measurement accuracy of the MTR-IR method for determination of cOi and cCs in single crystalline silicon materials.
The interference fringes become much stronger when a silicon wafer thickness is close to the infrared wavelength. The fringes are well recognized to interrupt the IR measurement, they obscure the weak features of the spectra, as well as reduce the accuracy of quantitative analysis. Both IR and MTR-IR are able to measure a silicon slice with a thickness above 0.3 mm because the multiple beams resulted from multiple reflections and transmissions are out of phase and thus these beams generate neglectable interference fringes[29].
However, when the sample thickness is less than 0.2 mm, the interference fringes become more obvious and cannot be ignored when measuring Oi and Cs. The amplitude of interference fringes depends on the interaction mode between the incident light and the sample. Eq.(1), (3) and (4) are used to calculate the transmittance of three modes respectively: normal incidence, Brewster angle single transmission, and MTR. For the Brewster angle incidence, Rp is equal to 0, while Rs is 0.70. Obviously the oscillation of transmittance is derived from the phase change of ψ, thus the p-polarization does not cause any oscillation of transmittance at the Brewster angle incidence. In (1), the whole term affects the amplitude of oscillation, while in (3) and (4), the second term bearing the phase change of ψ becomes weaker and weaker when N increases. Therefore the amplitude of oscillations must be reduced with increasing N. In Fig. 5, the variation of oscillations caused by phase change (ψ) is shown for the normal incidence, the Brewster angle single transmission, and the MTR mode respectively. The amplitude of the oscillation is 0.058 for the normal incidence (T), 0.029 for the Brewster angle single transmission (TB), and only 0.002 5 for the MTR-IR approach (TMTR). In this case, theoretically compared to the normal incidence, the Brewster angle single transmission reduces the oscillation amplitude by a factor of 2, whereas, the MTR setup reduces the oscillation amplitude by a factor of 23. The above theoretical analysis demonstrates the overwhelming advantages of the MTR setup for measuring cOi and cCs in a thin silicon slice.
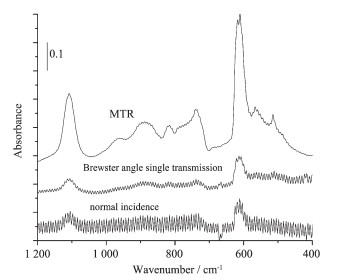
To prove the theoretical calculation, we recorded the spectra of a 0.20 mm thin silicon wafer in Fig. 6 with normal incidence (bottom trace as “normal incidence”), Brewster angle single transmission (middle trace as “Brewster angle single transmission”) and MTR (upper trace as “MTR”) respectively. From the three curves, it is easily observed that interference fringes appear heavily for the normal incidence, moderately for the Brewster angle single transmission, and negligibly for the MTR. The interference fringe strength ratios of MTR/Brewster angle single transmission/normal incidence are close to 20:2:1 in most regions.
From Fig. 6, not only the interference fringes in MTR-IR are greatly attenuated, the target signals in the region of 400 to 1 200 cm-1 are also significantly magnified. Thus the signal to noise ratio is enhanced several orders of magnitude higher in MTR for much thinner silicon slices less than 0.3 mm thickness. The use of a thin silicon wafer can decrease the sampling volume, save the cost of an experiment, and fits the requirements of the solar energy industry. From both the theoretical calculations of Fig. 5 and the experimental spectra of Fig. 6, obviously the currently used standard IR method is not suitable, whereas MTR-IR is much more powerful for measurement of Oi and Cs in a thin silicon slice less than 0.3 mm thick. That is also why MTR-IR is needed urgently for the silicon solar cell industry.
Finally, we present the evolution of 7 infrared traces against N in Fig. 7a. We have demonstrated the linear relationship of the absorbance strength of a band against the number of simplified transmission times (N) in our previous report [23]. Since the detection limit of an analysis method depends on the signal to noise ratio. For the measurements of Fig. 3 and Fig. 7a, their baselines are flat enough, therefore, we can assign the spectral noise from 0.3~2.0 mm thick silicon samples to the instrumental noise, which possess the same value. With this hypothesis, we can deduce the detection limits of Oi and Cs, shown in Fig. 7b, at different N from 6 to 12 by dividing the standard detection limits with the peak magnification times of MTR/normal incidence (peak height of Oi or Cs in Fig. 7 /peak height of Oi or Cs in IR-sample in Fig. 3). It is observed that our MTR-IR method significantly improves the detection limits of cOi and cCs for the standard 2.0 mm thick single crystalline silicon, reaching cOi and cCs at 1×1015 and 5×1014 cm-3, respectively.
3 Conclusions
In conclusion, our experiments confirm that the MTR-IR method can reach a higher sensitivity and better spectral quality than the most commonly used conventional IR. The signal of the Oi peak at 1 107 cm-1 obtained by MTR can be enhanced 10 times than by the conventional IR method, the one of the Cs peak at 605 cm-1 8 times. The MTR sampling length is N(1+1/n2)1/2 times long as the one in the conventional IR, thus the measured cOi and cCs are more representative. Since MTR-IR reduces the interference fringes greatly for silicon slices with a thickness thinner than 0.3 mm, it will be the most powerful tool to characterize the ultrathin silicon wafers and therefore the portable and foldable silicon devices. Due to its simple operation, MTR-IR satisfies the practical needs in industrial applications, especially for semiconductor and silicon solar cell industries.
Several parameters still need improvement in further works. For example, the theoretical equations are deduced from the main light path, neglecting other multiple reflections and transmissions on silicon and gold mirrors. The MTR formulas still need more experimental data for calibration.
Considering the conclusion above, we believe that the MTR-IR method will be established as a standard method for measurement of interstitial oxygen and substitutional carbon for crystalline silicon materials.
Supporting information is available at http://www.wjhxxb.cn
-
-
[1]
Boyle R. Thermo Scientific Application Note, 2008, 50640:1-4
-
[2]
Craven R A, Korb H W. Solid State Technol., 1981, 24(7):55-61
-
[3]
Benson K E, Lin W, Martin E P. Semiconductor Silicon 1981. Pennington N.J.: Electrochem. Soc. Inc., 1981:33-48
-
[4]
Abe T, Kikuchi K, Shirai S, et al. Semiconductor Silicon 1981. Pennington N.J.: Electrochem. Soc. Inc., 1981:54-71
-
[5]
Rava P, Gatos H C, Lagowski J. Semiconductor Silicon 1981. Pennington N.J.: Electrochem. Soc. Inc., 1981:232-243
-
[6]
Ohsawa A, Honda K, Yoshikawa M. Fujitsu Scie. Techn. J., 1980, 16(3):123-134
-
[7]
Kishino S, Matsushita Y, Kanamori M. Appl. Phys. Lett., 1979, 35(3):213-215 doi: 10.1063/1.91098
-
[8]
Ogino M. Appl. Phys. Lett., 1982, 41(9):847-849 doi: 10.1063/1.93715
-
[9]
Oehrlein G S, Lindstrom J L, Corbett J W. Appl. Phys. Lett., 1982, 40(3):241-243 doi: 10.1063/1.93060
-
[10]
Ohsawa A, Takizawa R, Honda K, et al. Appl. Phys., 1982, 53(8):5733-5737 doi: 10.1063/1.331461
-
[11]
Pajot B. Analusis., 1977, 5:293-303
-
[12]
Hrostowski H J A B J. J. Chem. Phys., 1960, 33:980-990 doi: 10.1063/1.1731397
-
[13]
Corbett J W, Mcdonald R S, Watkins G D. J. Phys. Chem. Solids, 1964, 25:873-879 doi: 10.1016/0022-3697(64)90100-3
-
[14]
Kaiser W, Keck P H, Lange C F. Phys. Rev., 1956, 101(4): 1264-1267 doi: 10.1103/PhysRev.101.1264
-
[15]
Kaiser W, Keck P H. J. Appl. Phys., 1957, 28(8):882-885 doi: 10.1063/1.1722880
-
[16]
Kaiser W, Frisch H L, Reiss H. Phys. Rev., 1958, 112(5): 1546-1554 doi: 10.1103/PhysRev.112.1546
-
[17]
Bosomworth D R, Hayes W, Spray A R L, et al. Royal Soc. London, 1970, 317(1528):133-152 doi: 10.1098/rspa.1970.0107
-
[18]
Pajot B, Deltour J P. Infrared Phys., 1967, 7:195-200 doi: 10.1016/0020-0891(67)90018-8
-
[19]
Oeder R, Wagner P. Defects in Semiconductors Ⅱ. N.Y.: North-Holland, 1983:171-175
-
[20]
Kolbesen B O, Kladenovi T. Krist. Tech., 1980, 15(1):k1-k3 doi: 10.1002/(ISSN)1521-4079
-
[21]
ASTM. Designation F1188: Test Method for Interstitial Atomic Oxygen Content of Silicon by Infrared Absorption.
-
[22]
ASTM. Designation F1391: Test Method for Substitutional Atomic Carbon Content by Infrared Absorption.
-
[23]
Liu H, Xiao S, Chen Y, et al. J. Phys. Chem. B, 2006, 110 (36):17702-17705 doi: 10.1021/jp063467q
-
[24]
Guo P, Liu H, Liu X, et al. J. Phys. Chem. C, 2010, 114(1): 333-341 doi: 10.1021/jp909027e
-
[25]
Liu H, Venkataraman N V, Bauert T E, et al. J. Phys. Chem. A, 2008, 112(48):12372-12377 doi: 10.1021/jp804553x
-
[26]
Liu H, Venkataraman N V, Spencer N D, et al. Chemphyschem, 2008, 9(14):1979-1981 doi: 10.1002/cphc.v9:14
-
[27]
LIU Hong-Bo (刘洪波). Thesis for the Doctorate of Nanjing University(南京大学博士论文). 2008.
-
[28]
Xiao S, Liu H, Tobias B. China Patent, 2006, 10097859.4. 2006-11-16.
-
[29]
Leroueille J. Appl. Spectrosc., 1982, 36(2):153-155 doi: 10.1366/0003702824638890
-
[30]
Baghdadi A, Bullis W M, Croarkin M C, et al. J. Electrochem. Soc., 1989, 136(7):2015-2024 doi: 10.1149/1.2097135
-
[1]
-
Scheme 1 Scheme of the MTR-IR optical path
The incident light, depicted with arrows, transmits the silicon chip N times and reflects on two gold mirrors N times too, finally reaches the detector. The parameters used in the calculation are marked: b, the thickness of the chip; θ, the Brewster incidence angle of 74°; bB, the optical path at the Brewster incidence[27-28].
Figure 3 Comparison of Oi and Cs spectra for MTR-IR and conventional IR
Length of the sample is 50 mm, n=3.42, N=10, b=0.045 cm, θ=74°. "MTR-sample" denotes the spectrum of a sample measured with the MTR-IR method; "IR-sample" indicates the spectrum of the same sample measured with the conventional IR method
Figure 4a Oi concentration at 1 107 cm-1 for eight samples measured by MTR-IR vs conventional IR
cOi=3.14×1017×εOi (cm-3)[21]
Figure 4b Cs concentration at 605 cm-1 for eight samples measured by MTR-IR vs conventional IR
cCs=8.2×1016×εCs (cm-3)[22]
Figure 5 Theoretical simulation of the transmittance oscillations as a function of the wavenumber σ calculated from Eq.(1), (3) and (4), corresponding to the normal incidence, the Brewster angle single transmission and MTR respectively
With assignment of n=3.42, ε=39.5 cm2, b=0.02 cm, bB=0.020 8 cm, bMTR=0.166 4 cm, θ=74°, N=8
-

 扫一扫看文章
扫一扫看文章
计量
- PDF下载量: 2
- 文章访问数: 381
- HTML全文浏览量: 34





 下载:
下载:








 下载:
下载:

