English

• 终点误差是滴定分析的核心内容之一，对于滴定方法的理论研究以及实验设计都有重要指导作用。另外，终点误差涉及化学平衡的综合性知识，是高等分析化学课程的学习重点和难点。

  在现行分析化学教材中，四大滴定的终点误差计算没有统一，计算公式众多，不仅加重记忆负担，而且无法用于某些复杂滴定体系。很多研究致力于通过林邦公式统一终点误差的计算，并且取得了一定的成果，然而，林邦公式只是近似公式，只有在滴定终点和化学计量点接近时才比较准确，并且仅适用于反应物化学计量关系为1 :1的滴定反应。由于林邦公式的以上局限性，终点误差计算没有真正实现统一^[1~5]。

  笔者在《滴定分析终点误差的通用高效计算策略》^[6](简称“策略”文，下同) 中提出以体积定义式代替传统的浓度定义式，以实现终点误差计算的统一和准确滴定判别的统一。囿于篇幅，“策略”文没有给出这两种定义式等价的证明，因此导致某种误解：以为体积定义式并非普适，如闭凤丽等^[7]在《滴定分析终点误差计算公式之探讨》(简称“探讨”文，下同) 中提到：“邵利民建立了直接以体积来计算终点误差，方法虽然简便，但是仅限于等浓度的情况，应属于式 (12) 的一个特例。”

  本文给出了体积定义式与浓度定义式完全等价的理论证明；一方面为通过体积定义式统一终点误差进一步提供支持，另一方面也澄清了体积定义式在普适性方面可能存在的误解。此外，选取了3本具有代表性的分析化学教材，梳理、归纳出当前分析化学课程体系中终点误差的处理方法；剖析了终点误差处理策略的现状以及林邦公式的局限性。

  1   终点误差的定义

  1.1   终点误差的几种定义式

  分别以X和T表示被测物和滴定剂，二者的分析浓度分别表示为c_X和c_T；滴定反应的化学计量关系为：n X~m T；以V_X表示被测物溶液体积，分别以V_ep和V_sp表示滴定剂在滴定终点和化学计量点时的加入体积。

  对于上述滴定体系，传统的终点误差定义式 (即浓度定义式) 为：

  其中，c_T^ep和c_X^ep分别表示滴定剂和被测物在终点时的分析浓度。

  “策略”一文提到的终点误差体积定义式为：

  “探讨”一文提到的终点误差体积比定义式为：

  其中，ρ_ep=V_ep/V_X，ρ_sp=V_sp/V_X。

  关于上述3种定义式，有以下几点值得注意：

  绝大部分国内教材采用浓度定义式，即式 (1)；“策略”文提到以R=V_ep/V_sp，看起来也是一种体积比，目的是减少一个变量，以方便计算；“探讨”文中提及的终点误差定义式 (文中式 (10)) 实际上是式 (1) 在m=n情况下的特例。

  1.2   终点误差定义式之间的关系

  终点误差的上述3种定义式完全等价，下面给出证明。

  1.2.2   体积定义式与体积比定义式等价

  根据体积比的定义，可得ρ_ep=V_ep/V_X，ρ_sp=V_sp/V_X，将之代入式 (3) 即可得到式 (2)：

  所以，终点误差的体积定义式与体积比定义式等价。

  1.2.1   体积定义式与浓度定义式等价

  终点时，滴定体系的体积为 (V_ep+V_X)，因此根据c_T^ep和c_X^ep的含义，可以得到：

  将以上二式代入式 (1)，整理后得到：

  在化学计量点时，被测物X和滴定剂T恰好完全反应，其物质的量符合滴定反应的化学计量关系n X~m T，所以：

  将式 (5) 代入 (4)，即可得到体积定义式：

  所以，终点误差的体积定义式与浓度定义式等价。

  值得指出的是，上述证明过程中没有引入条件c_T=c_X，所以，体积定义式并不如“探讨”一文中所说的“……但是仅限于等浓度的情况，应属于式 (12) 的一个特例”(该文所指“式 (12)”即是体积比定义式)。

  2   终点误差的计算

  绝大多数国内分析化学教材中，终点误差通过浓度定义式来定义，然而，浓度定义式包含4个参数，参数较多且随着滴定体系的不同而改变，因此不方便直接计算终点误差。为了解决这一问题，研究者 (基于浓度定义式) 推导出了效率较高的计算公式，最具代表性的当属EDTA配位滴定中的林邦公式。

  采用导出公式来计算终点误差是当前分析化学教材的通行做法。由于滴定体系的不同和推导方式的差异，所以存在多个导出公式，客观上造成了计算公式众多、计算策略各异的复杂局面。为了剖析这种复杂局面，选取了3本教材，对其终点误差计算进行了总结，结果列于表 1。这3本教材分别是武汉大学主编的《分析化学》第五版 (“十一五”国家级规划教材，面向二十一世纪课程教材)^[8]，华中师范大学等六校合编的《分析化学》第四版 (面向二十一世纪课程教材)^[9]，以及李龙泉等编著的《定量化学分析》第二版 (中国科学院指定考研参考书)^[10]。这3本教材具有一定的代表性，因此表 1基本可以反映当前分析化学课程体系中终点误差的计算策略。

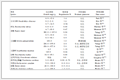  表 1  三本国内教材中四大滴定的终点误差处理模式^a Table 1.  Different strategies of computing titration error in three textbooks in China

  表选项

  导出Excel

  下载全尺寸表图像

  表 1中的“林邦公式”特指Ringbom导出的用于计算EDTA配位滴定终点误差的公式^[11]。该公式拓展到其他滴定体系时，需要进行修正，这就是表中提及的“类林邦公式”。

  “武大版”在酸碱滴定、配位滴定和氧化还原滴定的终点误差计算中，均采用林邦公式或者类林邦公式，看上去最为统一。但是仍然存在多个计算式，例如一元酸、多元酸和混合酸滴定体系的类林邦公式并不相同。此外，对于某些复杂体系，如不对称电对的氧化还原滴定，教材中没有提供相应的类林邦公式 (有人推导出了这一公式^[12]，形式过于复杂，实用价值不高)。可见，这种统一是不完全的，形式相近的计算公式并没有提高计算效率。

  “华中师大版”的终点误差计算较为简单，仅涉及四大滴定中的酸碱滴定和配位滴定，而在酸碱滴定中也只是介绍了一元酸 (碱) 滴定体系。值得注意的是，尽管只涉及了两种滴定体系，该教材也没有采用统一的计算策略。

  “科大版”的终点误差计算最为全面，四大滴定全部涉及；在氧化还原滴定中，除了对称电对之外，还介绍了不对称电对滴定的终点误差计算。“科大版”仅在配位滴定使用了林邦公式，而在酸碱滴定和氧化还原滴定中，使用了从浓度定义式导出的计算公式 (非林邦公式形式，多个公式)。

  武汉大学版《分析化学》属于经典，其内容常为其他教材所借鉴，“华中师大版”和“科大版”即是如此。然而，在终点误差的处理方面，这两本教材却与“武大版”大相径庭，没有刻意通过林邦公式统一计算。这一方面说明了终点误差计算策略的复杂性，另一方面也表明“以林邦公式统一终点误差”这种处理方式没有明显的优越性。

  3   终点误差计算的统一

  统一终点误差计算的重要性不言而喻。以林邦公式进行统一是一种常见策略，相关研究文献很多，也取得了一些有价值的成果，“武大版”教材即采取这种策略。如前所述，这种策略其实没有实现完全统一：不同滴定体系的类林邦公式仍不相同，尽管形式相近。另外一些研究旨在提高统一程度，为此引入多个参数 (以适应不同滴定体系)，进而推导出一个接近普适的类林邦公式，但是公式异常复杂，实用价值很低。

  以林邦公式统一终点误差的策略陷入一种困境：提高统一程度却增大了相应算式的复杂性；对算式进行简化却又降低了通用性，不得不增加简化算式的数量以适用于不同的滴定体系。即使在算式的通用性和复杂性之间取得平衡，达到形式上的某种统一，但是也没有完全走出这个困境。

  上述困境的直接原因是林邦公式是一个适用范围有限的公式：仅能用于化学反应计量关系为1 :1的滴定反应^[13]。在更深层次上，上述困境可能源于分析化学经典课程体系中的“公式化”思路，即为某类问题提供一个计算公式，强调计算的可完成性。在教学中，这种“公式化”策略会导致两个严重问题，一是“按图索骥”式的解题方法失之灵活，难免机械套用；二是无法解决一些复杂问题，因为无公式可用 (如下面例题2)。

  为了摆脱上述困境，真正实现终点误差的统一计算，需要一个通用同时具有良好计算性的公式。1.1节中介绍的体积定义式能够满足这些要求。通过体积定义式计算终点误差的实质是：将终点时平衡体系的基本等量关系，如电荷平衡、物料平衡或者能斯特方程，转化为关于R (R=V_ep/V_sp) 的代数方程，解之即可。这个代数方程多数情况下是关于R的一元代数方程，所以运算量比较小。下面通过一些例题进行说明，例题均选自文献^[13]，部分数值略有修改。

  例1：用0.10mol/L的NaOH溶液滴定0.050mol/L的H₃PO₄溶液，滴定至第二化学计量点，以百里酚酞为指示剂，终点为pH_ep=10.0。计算终点误差 (K_a1=7.6×10^-3，K_a2=6.3×10^-8，K_a3=4.4×10^-13)。

  解  分别用V_ep和V_sp表示滴定终点和化学计量点时加入NaOH溶液的体积，并令R=V_ep/V_sp。根据反应物浓度和滴定反应的计量关系，易知被测物溶液的体积等于V_sp，因此，终点时溶液的总体积等于 (V_ep + V_sp)。

  终点时体系的电荷平衡方程 (Charge balance equation，CBE) 如下：

  通过分布分数将上式中的[H₂PO₄^-]_ep、[HPO₄^2-]_ep和[PO₄^3-]_ep表示为关于[H⁺]_ep的代数式，得到式 (6)：

  易知：[Na⁺]_ep=0.10V_ep/(V_ep+V_sp)=0.10R/(R+1)，c_{H3PO4, ep}=0.050V_sp/(V_ep+V_sp)=0.050/(R+1)，将以上参数代入 (6) 式，整理后得到关于R的一元方程：R=(0.050a+b)/(0.10-b)，其中：

  解之可得R=1.0034，进而求得终点误差E_t=(R-1)×100%=0.34%。

  如果滴定到第一化学计量点，甲基橙作为指示剂，pH_ep=4.4，那么解题思路不变，通过终点时CBE得到的定量关系仍然是式 (6)，只是被测物溶液的体积等于2V_sp，终点时溶液的总体积等于 (V_ep+2V_sp)，相应参数如下：

  将以上参数代入式 (6)，整理后得到关于R的一元方程，解之可得R=0.9952，进而求得终点误差E_t=(R-1)×100%=-0.48%。

  NaOH对H₃PO₄的滴定体系，滴定到第一化学计量点和第二化学计量点实质上没有区别，然而在传统的、基于浓度定义式的终点误差计算中，各自的计算公式差别很大，而且形式复杂^{[8, 10]}。

  例2：在pH=6.0的缓冲溶液中，通过配位滴定测量溶液中14种镧系离子的总量。滴定剂为0.028mol/L的EGTA溶液，14种镧系离子的浓度均为0.0020mol/L。以二甲酚橙为指示剂，并且设滴定终点仅由LaIn决定。计算终点误差。(pLa_t|_{二甲酚橙, pH=6.0}=5.6，α_{Y (H)}|_pH=6.0=4.47×10⁴，按照周期表顺序，14种镧系离子的K_MY分别为3.55×10¹⁵，5.01×10¹⁵，1.12×10¹⁶，1.91×10¹⁶，7.59×10¹⁶，1.26×10¹⁷，8.71×10¹⁶，1.86×10¹⁷，2.63×10¹⁷，2.40×10¹⁷，2.51×10¹⁷，3.02×10¹⁷，6.02×10¹⁷，6.46×10¹⁷)。

  分析  终点时溶液中存在多种金属离子，但是只有La的浓度已知，所以，必须消去物料平衡中含有其他金属离子的项，这可以借助分布分数来实现。

  解  分别用V_ep和V_sp表示滴定终点和化学计量点时加入EGTA溶液的体积，并令R=V_ep/V_sp。根据反应物浓度和滴定反应的计量关系，易知被测物溶液的体积等于V_sp，因此终点时溶液的体积等于 (V_ep+V_sp)。

  终点时关于EGTA的物料平衡方程 (Mass balance equation，MBE) 为：

  通过分布分数，消去上式中的各配离子浓度，得到：

  其中，c_{M, ep}表示溶液中14种镧系离子在滴定终点时的分析浓度；易知，c_{M, ep}=0.0020/(R+1)。

  另外一个条件是[La′]_ep=10^-5.6。结合K′_LaY以及La的MBE，得到：

  通过以上两式消去R，简单整理后得到关于[Y′]_ep的方程：

  其中，A=K′_LaY[Y′]_ep 1+K′_LaY[Y′]_ep +…+ K′_LuY[Y′]_ep 1+K′_LuY[Y′]_ep。

  通过文献^[13]的附录程序iroots在[10^-9，10^-8]范围内搜索，得到[Y′]_ep的双精度数值为5.00128×10^-9，进而计算得到R=0.99957。所以，终点误差E_t=(R-1)×100%=-0.043%。

  通过以上两道例题可以看出，体积定义式是一种通用的终点误差计算方法，记忆负担很轻，运算量也不大。对于例题1，通过类林邦公式也能够求解^[8]；对于例题2，类林邦公式或者其他公式则无能为力。

  4   结论

  终点误差目前广泛采用的计算策略是以浓度定义式为基础，推导出各种便于计算的公式。而终点误差体积定义式等价于传统的浓度定义式，并具有形式直观、计算高效的优点，能够统一四大滴定的终点误差计算。此外，体积定义式具有良好的计算实用性，不再需要进一步推导计算式，因此是一种“去公式化”的终点误差计算策略。并且，体积定义式能够计算传统方法无能为力的复杂问题，而林邦公式仅适用于简单滴定体系的终点误差计算，不适合终点误差的统一。

• 1. [1]

     陶德祥.化学通报, 1990, 53(10):54-55. http://www.cqvip.com/QK/94692X/199010/286997.html

  2. [2]

     陈兴国, 寇宗燕, 胡之德.大学化学, 1991, 6(3):54-56. http://www.cnki.com.cn/Article/CJFDTotal-DXHX199103019.htm

  3. [3]

     王园朝, 包海峰.大学化学, 2013, 28(3):82-86. http://www.cnki.com.cn/Article/CJFDTotal-DXHX201303018.htm

  4. [4]

     刘少英.大学化学, 1990, 5(2):50-51. http://www.cqvip.com/QK/96492X/199002/225257.html

  5. [5]

     龚兆胜, 黄红苹.大学化学, 2010, 25(6):69-72. http://www.cnki.com.cn/Article/CJFDTotal-DXHX201006019.htm

  6. [6]

     邵利民.化学通报, 2012, 75(10):952-956. http://www.cnki.com.cn/Article/CJFDTotal-HXTB201210020.htm

  7. [7]

     闭凤丽, 尹华勤, 甘峰.化学通报, 2015, 78(9):859-863. http://www.hxtb.org/ch/reader/view_abstract.aspx?file_no=20141228001&flag=1

  8. [8]

     武汉大学主编.分析化学 (第五版).北京:高等教育出版社, 2006.

  9. [9]

     华中师范大学等6校合编, 分析化学 (第四版).北京:高等教育出版社, 2011.

  10. [10]

      李龙泉, 朱玉瑞, 金谷等.定量化学分析 (第二版).合肥:中国科学技术大学出版社, 2005.

  11. [11]

      A Ringbom. 1963. Complexation in Analytical Chemistry:A Guide for the Critical Selection of Analytical Methods Based on Complexation Reactions. New York:Interscience

  12. [12]

      梁保安, 郭德敏, 刘永和.许昌师专学报, 1992, 11:41-49. http://www.cqvip.com/Main/Detail.aspx?id=916281

  13. [13]

      邵利民.分析化学.北京:科学出版社, 2016.

• 表 1  三本国内教材中四大滴定的终点误差处理模式^a

  Table 1.  Different strategies of computing titration error in three textbooks in China

  下载: 导出CSV
•