English

• Recently, a novel 2D BC₂P monolayer material has been reported, which is of great significance for the study of high-performance anode materials and carbon dioxide adsorption materials [1]. 2D materials have unique vibrational, electronic, optical, magnetic and topological behaviors [2–5]. Therefore, they have broad application potential in many fields, and may also bring new electronic devices and technologies, such as spintronics, catalysis and thin film technology [6]. In addition, the discovery and synthesis of materials with 2D functions have always been the focus of chemical, physical and material science research [7–10].

  Data-driven new material discovery is becoming one of the most promising material design methods [11,12]. In recent years, high-throughput screening based on DFT has achieved amazing success. A large number of 2D materials with functional properties have been discovered by this method [13]. The application of various screening algorithms, such as chemical substitution, alternative site modification, and crystal structure prediction, has expanded the list of 2D materials and accelerated the discovery of 2D materials [14,15]. However, the high computational cost and poor scalability of DFT limit its application in chemical and structural spaces [16]. The effective inverse design of new materials is to achieve the mapping of target properties to atomic structures [8]. Previous studies have focused on screening known materials, using global optimization algorithms to search for chemical structures [17], or generating new materials by element substitution of known materials [18]. An obvious limitation of this method is that the obtained materials are similar to the reference materials to some extent. Even if the type of atoms or ions is changed during lattice modification [19], they still satisfy the same space group, occupied Wyckoff position and stoichiometric ratio.

  Deep generative model (DGM) provide new ways to address the limitations of the lattice decoration paradigm [20]. Recently, Xie et al. proposed a CDVAE model [21]. The model uses a VAE and a diffusion model to generate materials during the diffusion process by learning the data distribution of stable materials. The model can directly process the atomic coordinates and learn the continuous representation of the structure, eliminating the need for intermediate representations such as graphics or descriptors, and using the equivariant graph neural network to ensure that the output results have the same properties under different transformations.

  In this work, we trained a CDVAE model for the BCP material proposed by Fu et al. [1], and generated 10,000 new structures. After screening out the candidate structures through validity and diversity checks, the M3GNet [22] was used as a pre-trained model for structural relaxation. After narrowing the range of candidate structures, we excluded materials that did not meet the BCP bonding specifications, and performed a complete DFT calculation on the remaining materials to evaluate the thermodynamic and kinetic stability of these newly generated materials. In general, the structure generated by CDVAE has similar or even higher cohesive energy values than the training data, but there are obvious differences in element composition and crystal structure. Therefore, we believe that the DGM can explore and generate the material structure and composition that have not been involved before by considering a wider phase space, which brings new possibilities for material design.

  Our computational workflow, as illustrated in Fig. 1, comprises three main components. The first component involves the database and DGM utilized in this study. The composition of elements in the database and the corresponding atomic quantities are displayed in the BCP Database. The second component focuses on the generation and initial screening of new materials. The third component involves the computation of various properties for the generated materials. CDVAE is a structure generation method based on diffusion model, M3GNet is a structure relaxation method based on graph neural networks, and DFT relaxation is a first-principles calculation method.

  Figure 1

  

  Figure 1.  It shows the complete inverse design workflow of the new 2D BCP using the CDVAE model, M3GNet and DFT. The left column shows the training data used as well as the training model, and the middle column shows the preliminary screening and structural relaxation of the generated structure. The right column shows the attribute analysis after calculation using DFT. In CDVAE, the input crystal can be represented by a tuple, which consists of the atomic number A of N atoms, their respective coordinates X, and the base vector L of the crystal cell. The base vector describes the shape and size of the repeating units of the crystal structure. In M3GNet, the material graph includes bond length information ε, atomic information v, coordinate information x, lattice information M, and optional global state information.

  DownLoad: Full-Size Img PowerPoint

  We employed a pre-trained deep learning model, M3GNet, for structure relaxation to accelerate the prediction of new materials. M3GNet consists of feature extraction, many-body computations, and graph convolutions as the main computational modules. It predicts the formation energy, forces, and stresses of materials by M3GNet model. During the relaxation process, the M3GNet algorithm considers all atomic coordinates and a 3 × 3 lattice matrix, sequentially updating attributes of bonds, atoms, and states. After performing these operations, we used DFT calculations to relax structures that met the BCP bonding specifications, and their thermodynamic stability was verified using cohesive energy. We also evaluated the dynamic stability through phonon calculations at high symmetry points. As a measure of success for CDVAE inverse design, we analyzed the chemical composition and structural diversity of the generated materials.

  The CDVAE model is a generative model that combines VAE [23] and diffusion model [24] to generate stable materials. The model consists of an encoder, attribute predictor, and decoder. The encoder uses a SE(3)-equivariant periodic graph neural network (PGNN) [25] to map the input atomic coordinates and types from high-dimensional space to a low-dimensional latent representation space. The attribute predictor employs one-dimensional dilated convolutions with residual connections in lieu of the traditional multilayer perceptron. The network defines three modules: ResidualBlock, DilatedConvBlock, and Conv1d. Following each convolution operation, batch normalization and ReLU activation function are applied, introducing shortcut connections that allow gradients to flow directly to shallower layers. This facilitates the transmission of information and enhances learning efficiency, enabling an effective increase in the model's receptive field and learning capacity while maintaining a relatively low number of parameters and computational complexity. By progressively increasing the dilation rate, the model is capable of capturing features across different scales. The decoder part uses a noise-conditioned score network (NCSN) [26] to receive the noisy latent representation and learns denoising to generate atomic coordinates and types. Based on the information of neighboring atoms, the latent representation is reconstructed into the final stable structure by updating the atom type by applying gradients to the atomic coordinates. The detailed architecture of the network is illustrated in Fig. 2.

  Figure 2

  

  Figure 2.  Main parts of the CDVAE architecture. The (a) encoder and (b) decoder networks are primarily divided into three modules: The embedding module, the interaction module, and the output module. The embedding module takes the type of atoms and the distances between them as input, converting the atom types into learnable feature vectors. The interaction module facilitates the transmission of information and the update of features, whereas the role of the output module is to transform and accumulate the message embeddings from each embedding block, yielding the final prediction results. (c) The improved attribute predictor network.

  DownLoad: Full-Size Img PowerPoint

  To simulate uncertainty and perturbation effects that exist in materials, noise is added to atomic types and coordinates. The attribute predictor is used to predict the composition, lattice, and number of atoms in the crystal, and a unit cell is constructed based on the predicted basis vectors. Next, positions are randomly selected in the unit cell, and the predicted atoms are placed at these random positions. The decoder gradually denoises the randomly placed atoms’ types and coordinates to make them similar to the data distribution of the training set. During the generation process, Langevin dynamics is used for progressive deformation to simulate the random motion of particles in a potential energy field and gradually approach the equilibrium state. By applying Langevin dynamics, the atoms of the material iterate towards energy minimization direction based on their current position and gradient information until a stable structure is reached.

  The design principle of the CDVAE model is to generate 3D periodic materials, however, our goal is to further explore in the chemical space of predicted 2D materials to generate novel 2D materials. To address the problem that 2D materials are non-periodic in one direction, we introduced artificial periodicity according to the method mentioned in the literature [8]. Specifically, the size of the lattice vector in the non-periodic direction is one order of magnitude larger than that in the periodic direction. We increase the cutoff radius from 7 Å to 10 Å for the graph network in the decoder. This ensures that the graph network only connects atoms in the 2D layer, allowing CDVAE to learn to generate 2D materials. The model incorporates a loss function comprising cross-entropy and mean square error losses, while utilizing the Adam optimizer [27]. To manage the learning rate, a learning rate adjustment strategy is applied through the ReduceLROnPlateau scheduler. The initial learning rate is set at 0.001, with a minimum value of 0.0001, aiding in controlling optimization step sizes and preventing overfitting. In the attribute predictor, all three modules discussed in this study are characterized by a channel count of 256. Notably, the final Conv1d output channel is set to 25, with a kernel size of 3 × 1. The parameters for stride and padding remain at their default values of 1 and 0, respectively.

  Given the vast number of BCP materials generated, conducting full DFT calculations on each structure is impractical due to high costs. To efficiently assess these materials, we utilized multiple criteria for screening and evaluation. Initially, we checked the structures’ validity against pre-defined effectiveness standards, considering both their structure and composition. For structural validity, we followed Court et al.’s method [28], deeming structures with any atom pair distanced over 0.5 Å as valid. This criterion mainly focuses on atomic distances, omitting other factors. Compositionally, we applied the SMACT calculation method to verify material charge neutrality. Materials were considered compositionally valid if SMACT calculations confirmed a balanced overall charge, indicating neutrality.

  To check for duplicate structures in the generated structures, the StructureMatcher from pymatgen was used. The StructureMatcher measures the geometric difference between two structures by calculating their Root Mean Square Distance (RMSD) [29]. Specifically, the RMSD represents the average deviation between the corresponding atomic positions in two structures, calculated as follows:

  (1)

  Among them, N represents the total number of atoms, is the coordinate of the i-th atom in the structure being compared, is the coordinate of the corresponding atom in the reference structure. In the process of structure deduplication, we adopted the method mentioned in reference [30]. If the RMSD between two structures is less than 0.3 Å, it means that their geometric differences are small and they can be considered duplicates. Out of 10,000 structures generated by CDVAE, 387 were disqualified due to not meeting chemical formula or energy distribution criteria, leaving 9,613 for further study. Post-repeatability checks, only 1,689 remained unique, highlighting a high duplication rate possibly linked to the small training dataset and its inherent repetitions.

  To minimize DFT calculation costs, M3GNet was employed for rapid and accurate structural relaxation and energy prediction of the remaining structures (Fig. 3). The CDVAE-generated structures displayed lower energy levels and more diverse stoichiometries compared to the original dataset. Further DFT calculations adjusted atomic coordinates and lattice lengths to identify the most stable configurations, minimizing ground-state energy. This revealed changes in atomic coordinates and energies, suggesting the generated crystals were not at their energy surface's lowest points. This discrepancy arises because, unlike the training data relaxed through DFT, CDVAE was not trained to pinpoint structures near the energy surface's local minima, necessitating DFT relaxation for the generated structures. In addition, to demonstrate the effectiveness of M3GNet in relaxing structures and predicting their energies, crystal graph convolutional neural network (CGCNN) [31] was introduced as a comparative algorithm (Table 1). Error 1 represents the percentage error between the cohesive energy predicted by M3GNet and the cohesive energy obtained from DFT calculations. Error 2 represents the percentage error of the CGCNN algorithm. The results show that the cohesive energy prediction error of M3GNet is generally within 0.2 eV/atom, while the prediction error of CGCNN is significantly higher than this value. The data in the last column of the table represents the energy difference between the initial configuration and the final configuration of the generated structures during relaxation.If the initial structure of the material is reasonable, then the energy reduction after DFT relaxation should be relatively small. The difference between the initial energy and final energy of the successfully relaxed materials was mainly within the range of 0.1-0.3 eV/atom, indicating that the initial structures generated by the deep model are reasonable. Therefore, the CDVAE-generated structures are somewhat accurate and reliable in meeting the requirements of the material's ground-state energy, and M3GNet can be used as a method to speed up the generation of new structures. It is important to note that the purpose of this stage was to prove that M3GNet has the ability to be used as a structure relaxation algorithm and accurately predict the cohesive energy of structures.

  Figure 3

  

  Figure 3.  Cohesive energy distribution of each atom in the BCP structure. (a) The cohesive energy of the original BCP data with most structures concentrated within -5.5 eV/atom to -6.5 eV/atom range. (b) The cohesive energy of the CDVAE generated structures, predicted by the pre-trained deep learning model M3GNet, with most of the generated structures having cohesive energy within -6.5 eV/atom to -7.5 eV/atom range.

  DownLoad: Full-Size Img PowerPoint

  Table 1

  

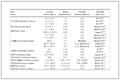  Table 1.  Comparison of results between the two prediction algorithms and the energy difference during structure relaxation (per atom).

  DownLoad: CSV

  As a final step in the preliminary screening, we manually removed materials that did not comply with the BCP bonding rules [32]. The CDVAE model generated a significant number of structurally unrealistic and chemically diverse structures, which can be attributed to the sampling process from a Gaussian distribution. It assumes that the distribution of atomic numbers and compositions follows a Gaussian distribution, while in reality, material distributions often deviate from Gaussian distributions and exhibit large variations and outliers.

  Finally, we used a density functional theory molecular dynamics simulation method and performed calculations using the Vienna ab initio simulation software package (VASP). In the calculation, the interaction between ions and electrons was modeled using projection enhanced wave (PAW) potential energy, and the Perdew Burke Ernzerhof approximation was used to describe the exchange correlation function. The truncation energy of the plane wave basis set is set to 500 eV. We use a Monkhorst Pack grid with a density of 0.03 Å⁻¹ to sample the Brillouin zone. By adjusting the kinetic energy truncation and k-point sampling, the total energy of each atom converges to less than 1 meV. In molecular dynamics simulations, we use phonon dispersion calculations to evaluate the dynamic stability of monolayers, which are implemented using the finite displacement method in the PHONOPY software package [33].

  The CDVAE-generated most stable BCP structure examples are shown in Fig. 4. It is evident that CDVAE is capable of generating structures distinct from the original data. In graphene, the length of the C-C bond is 1.42 Å, which is equivalent to the radius of a sp² hybridized carbon atom. The C-C bond lengths in the generated structures are all less than 1.5 Å. We believe that shorter C-C bond lengths indicate a tighter atomic arrangement and stronger interatomic interactions, leading to higher cohesive energy values. While cohesive energy alone cannot determine the relative stability of different atomic compositions, higher cohesive energy values can serve as evidence for strong bonding in these generated structures.

  Figure 4

  

  Figure 4.  Examples of the most stable structures generated by CDVAE. All generated structures have undergone complete DFT calculations and have high binding energy values. The green, pink, and gray dots represent boron, phosphorus, and carbon atoms, respectively. Among them, (b) and (e) all have flat graphene-like structures.

  DownLoad: Full-Size Img PowerPoint

  To further evaluate the dynamic stability of the generated structures, we calculated the phonon dispersion of the BCP monolayer. The phonon spectrum of BC₂P is shown in Fig. 5a, where negative eigenvalues represent imaginary phonon frequencies, indicating the possibility of structural reconstruction and instability within the original unit cell. To accurately assess stability, we considered the zero-frequency translational mode and numerical errors and used a threshold of eigenvalues greater than -0.01 meV/Å as the criterion for dynamic stability. Clearly, the phonon branches do not contain any imaginary frequencies, confirming the dynamical stability of the studied monolayer materials.

  Figure 5

  

  Figure 5.  The thermodynamic and dynamical stability analysis diagram of the BCP structure. (a) Phonon dispersion of the BC₂P monolayer. The high symmetry points are Г(0, 0, 0), Y(0, 0.5, 0), S/N(0.5, 0.5, 0) and X(0.5, 0, 0). (b) Energy oscillations of the MD simulation at room temperature for the 3 × 3 × 1 supercell of BC₂P monolayer.

  DownLoad: Full-Size Img PowerPoint

  After assessing the stability of the material based on energy and phonon spectra, we further examined the thermal stability of the BC₂P monolayer material at a temperature of 300 K using first-principles molecular dynamics (MD) simulations. The MD trajectory analysis (Fig. 5b), demonstrates that all structures can maintain their integrity at 300 K, exhibiting highly stable temperature and energy profiles. This validates the thermal stability of the generated BC₂P monolayer material. These findings contribute to advancing the research on experimental synthesis of 2D BC₂P monolayer materials.

  When assessing the success of inverse design via the CDVAE method, a key metric is the diversity of generated materials’ crystal structures. To compare generated and original structures, we used the t-SNE algorithm for dimensionality reduction, analyzing statistical properties at each position in the crystal to describe the chemical environment around atoms. This includes analyzing neighboring atom types and distances, and employing radial distribution function (RDF) features to capture atom interactions within the structure. RDF calculates the probability density function of interatomic distances, outlining their interactions.

  Feature vectors were input into the t-SNE algorithm, mapping high-dimensional vectors into 2D space while preserving relative distances, thus maintaining the structural information of the original data. Fig. 6a displays the t-SNE embedding of generated and original structures. The original data's distribution (orange dots) shows concentrated structural features with variations across materials, limited by the original training data's chemical stoichiometries and material types, leading to structural similarities. Nonetheless, differences across various stoichiometries persist. The generated data (green dots) shows a broader feature distribution. Fig. 6b zooms into generated structures, revealing distinct clusters separate from original structures, indicating that while the generated structures share attributes with the original, they also display significant differences. This suggests the generative model can create novel structures not present in the training data, with the boundaries indicating greater diversity in the generated structures compared to the original ones.

  Figure 6

  

  Figure 6.  (a, b) The visualization of the structural distribution of the original training data and generated data using t-SNE dimensionality reduction. The t-SNE algorithm transforms high-dimensional crystal structure features into points on a 2D plane, enabling a more intuitive observation of the relationships between structures.

  DownLoad: Full-Size Img PowerPoint

  For a larger phase space, we searched the existing material databases to find these generated candidate materials. We searched C2DB, Materials Project, and OQMD, but none of these databases mentioned the structures discovered in this study. Additionally, we conducted a literature search to determine if these materials had been previously discovered. A BC₂P monomer material was reported [34]. However, the arrangement of these two structures is completely different. The shorter bond lengths and higher cohesive energy values in the generated structure demonstrate its tighter stability and greater suitability for experimental synthesis. Two types of BC₂P monomer materials were also reported [35,36], but they did not provide detailed numerical values for bond lengths and angles, and neither of them exhibited structures similar to those discovered in this study. The cohesive energy values in these references were lower than those found in our structures. Further details regarding the BC₂P comparisons are provided in Table 2. As for the remaining generated structures, they have not been reported before, further confirming that CDVAE is capable of exploring novel material combinations and structures, covering previously undiscovered regions in the phase space.

  Table 2

  

  Table 2.  Comparison of the BC₂P structure. Lattice constant a; bond lengths between B-C, C-C and C-P atoms; bond angles between B-C-B and C-P-C atoms; cohesive energy per atom.

  DownLoad: CSV

  In conclusion, we proposed a multi-step method based on DGM for discovering new 2D BCP monolayer materials to achieve inverse design of new BCP monolayer materials. The combination of DGM, deep learning property prediction, and DFT calculations has proven to be highly effective in generating new and stable materials. Based on the proposed method, we have successfully generated five novel BCP monolayer materials on three different BCP monolayers. In addition to a significant expansion of the known space of 2D materials, our work quantitatively evaluates CDVAE and establishes its superior performance in terms of two key criteria: the ability to learn to train the stable properties of structures and to generate structural diversity sexual ability. In fact, we generate structures with high cohesive energy values, and the stoichiometry of the generated materials spans a wide range of types. Compared to traditional methods, DGM do not require explicit specification of chemical compositions but instead learn distributions from existing data and generate new rational structures. This approach enables a wider exploration of chemical space and generates more reasonable material structures. The use of deep learning property prediction allows for screening and evaluation of the properties of newly generated materials before conducting DFT validation, thus saving time compared to traditional DFT validation and experimental research. By utilizing DGM and property prediction model, it becomes possible to discover materials with desired properties in unexplored material phase spaces, filling the gaps in previously unexplored areas of the phase space.

  Declaration of competing interest

  The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

  Acknowledgment

  This work was supported by the National Nature Science Foundation of China (Nos. 61671362 and 62071366).

  
  
• 1. [1]

     X. Fu, X. Cheng, C. He, et al., Phys. Chem. Chem. Phys. 25 (3) (2023) 2430–2438. doi: 10.1039/d2cp04941d

  2. [2]

     M. Turunen, M. Brotons-Gisbert, Y. Dai, et al., Nat. Rev. Phys. 4 (4) (2022) 219–236. doi: 10.1038/s42254-021-00408-0

  3. [3]

     A.R. Khan, L. Zhang, K. Ishfaq, et al., Adv. Funct. Mater. 32 (2022) 2105259. doi: 10.1002/adfm.202105259

  4. [4]

     Y. Mo, L. Liao, D. Li, et al., Chin. Chem. Lett. 34 (2023) 107130. doi: 10.1016/j.cclet.2022.01.023

  5. [5]

     B. Ryu, L. Wang, H. Pu, et al., Chem. Soc. Rev. 51 (2022) 1899–1925. doi: 10.1039/d1cs00503k

  6. [6]

     Y. Song, E.M.D. Siriwardane, Y. Zhao, et al., ACS Appl. Mater. Interfaces 13 (2021) 53303–53313. doi: 10.1021/acsami.1c01044

  7. [7]

     L. Shen, J. Zhou, T. Yang, et al., Acc. Mater. Res. 3 (2022) 572–583. doi: 10.1021/accountsmr.1c00246

  8. [8]

     P. Lyngby, K.S. Thygesen, Npj Comput. Mater. 8 (2022) 232. doi: 10.1038/s41524-022-00923-3

  9. [9]

     K.M. Wyss, D.X. Luong, J.M. Tour, Adv. Mater. 34 (2022) 2106970. doi: 10.1002/adma.202106970

  10. [10]

      P. Ares, K.S. Novoselov, Nano Mater. Sci. 4 (2022) 3–9.

  11. [11]

      Y. Zhao, M. Al-Fahdi, M. Hu, et al., Adv. Sci. 8 (2021) 2100566. doi: 10.1002/advs.202100566

  12. [12]

      C. Chu, Q. Xiao, C. He, et al., Chin. Chem. Lett. 35 (2024) 109186. doi: 10.1016/j.cclet.2023.109186

  13. [13]

      Z. Ren, S.I.P. Tian, J. Noh, et al., Matter 5 (2022) 314–335. doi: 10.1016/j.matt.2021.11.032

  14. [14]

      T. Yang, J. Zhou, T.T. Song, et al., ACS Energy Lett. 5 (2020) 2313–2321. doi: 10.1021/acsenergylett.0c00957

  15. [15]

      S. Lu, Q. Zhou, Y. Guo, et al., Adv. Mater. 32 (2020) 2002658. doi: 10.1002/adma.202002658

  16. [16]

      Y. Zuo, M. Qin, C. Chen, et al., Mater. Today 51 (2021) 126–135. doi: 10.1016/j.mattod.2021.08.012

  17. [17]

      Y. Chen, J. Zhu, Y. Xie, et al., Nanoscale 11 (2019) 9749–9755. doi: 10.1039/c9nr01315f

  18. [18]

      M.C. Sorkun, S. Astruc, J.V.A. Koelman, et al., Npj Comput. Mater. 6 (2020) 106. doi: 10.1038/s41524-020-00375-7

  19. [19]

      S. Manti, M.K. Svendsen, N.R. Knøsgaard, et al., Npj Comput. Mater. 9 (2023) 33. doi: 10.1038/s41524-023-00977-x

  20. [20]

      A. Karthikeyan, U.D. Priyakumar, J. Chem. Sci. 134 (2022) 1–20. doi: 10.1007/s12039-021-01987-2

  21. [21]

      T. Xie, X. Fu, O.E. Ganea, et al., arXiv (2021) arXiv:2110.06197.

  22. [22]

      C. Chen, S.P. Ong, Nat. Comput. Sci. 2 (2022) 718–728. doi: 10.1038/s43588-022-00349-3

  23. [23]

      D.P. Kingma, M. Welling, arXiv (2013) arXiv:1312.6114.

  24. [24]

      J. Ho, A. Jain, P. Abbeel, Adv. Neural. Inf. Process Syst. 33 (2020) 6840–6851.

  25. [25]

      J. Han, Y. Rong, T. Xu, et al., arXiv (2022) arXiv:2202.07230.

  26. [26]

      Y. Song, S. Ermon, Adv. Neural. Inf. Process. Syst. 32 (2019) 11918–11930.

  27. [27]

      D.P. Kingma, J. Ba, arXiv (2014) arXiv:1412.6980.

  28. [28]

      C.J. Court, B. Yildirim, A. Jain, et al., J. Chem. Inf. Model. 60 (2020) 4518–4535. doi: 10.1021/acs.jcim.0c00464

  29. [29]

      H. Moustafa, P.M. Lyngby, J.J. Mortensen, et al., Phys. Rev. Mater. 7 (2023) 014007. doi: 10.1103/PhysRevMaterials.7.014007

  30. [30]

      M.N. Gjerding, A. Taghizadeh, A. Rasmussen, et al., 2D Mater. 8 (2021) 044002.

  31. [31]

      T. Xie, J.C. Grossman, Phys. Rev. Lett. 120 (2018) 145301.

  32. [32]

      X. Fu, J. Guo, L. Li, et al., Chem. Phys. Lett. 726 (2019) 69–76.

  33. [33]

      A. Togo, F. Oba, I. Tanaka, Phys. Rev. B 78 (2008) 134106. doi: 10.1103/PhysRevB.78.134106

  34. [34]

      A. Bafekry, M. Naseri, M. Faraji, et al., Sci. Rep. 12 (2022) 22269.

  35. [35]

      M. Tang, C. Wang, U. Schwingenschlögl, et al., Chem. Mater. 33 (2021) 9262–9269. doi: 10.1021/acs.chemmater.1c02957

  36. [36]

      R. Muthaiah, F. Tarannum, R.S. Annam, et al., RSC Adv. 10 (2020) 42628–42632. doi: 10.1039/d0ra08444a

• 

  Figure 1  It shows the complete inverse design workflow of the new 2D BCP using the CDVAE model, M3GNet and DFT. The left column shows the training data used as well as the training model, and the middle column shows the preliminary screening and structural relaxation of the generated structure. The right column shows the attribute analysis after calculation using DFT. In CDVAE, the input crystal can be represented by a tuple, which consists of the atomic number A of N atoms, their respective coordinates X, and the base vector L of the crystal cell. The base vector describes the shape and size of the repeating units of the crystal structure. In M3GNet, the material graph includes bond length information ε, atomic information v, coordinate information x, lattice information M, and optional global state information.

  下载: 全尺寸图片 幻灯片
  

  Figure 2  Main parts of the CDVAE architecture. The (a) encoder and (b) decoder networks are primarily divided into three modules: The embedding module, the interaction module, and the output module. The embedding module takes the type of atoms and the distances between them as input, converting the atom types into learnable feature vectors. The interaction module facilitates the transmission of information and the update of features, whereas the role of the output module is to transform and accumulate the message embeddings from each embedding block, yielding the final prediction results. (c) The improved attribute predictor network.

  下载: 全尺寸图片 幻灯片
  

  Figure 3  Cohesive energy distribution of each atom in the BCP structure. (a) The cohesive energy of the original BCP data with most structures concentrated within -5.5 eV/atom to -6.5 eV/atom range. (b) The cohesive energy of the CDVAE generated structures, predicted by the pre-trained deep learning model M3GNet, with most of the generated structures having cohesive energy within -6.5 eV/atom to -7.5 eV/atom range.

  下载: 全尺寸图片 幻灯片
  

  Figure 4  Examples of the most stable structures generated by CDVAE. All generated structures have undergone complete DFT calculations and have high binding energy values. The green, pink, and gray dots represent boron, phosphorus, and carbon atoms, respectively. Among them, (b) and (e) all have flat graphene-like structures.

  下载: 全尺寸图片 幻灯片
  

  Figure 5  The thermodynamic and dynamical stability analysis diagram of the BCP structure. (a) Phonon dispersion of the BC₂P monolayer. The high symmetry points are Г(0, 0, 0), Y(0, 0.5, 0), S/N(0.5, 0.5, 0) and X(0.5, 0, 0). (b) Energy oscillations of the MD simulation at room temperature for the 3 × 3 × 1 supercell of BC₂P monolayer.

  下载: 全尺寸图片 幻灯片
  

  Figure 6  (a, b) The visualization of the structural distribution of the original training data and generated data using t-SNE dimensionality reduction. The t-SNE algorithm transforms high-dimensional crystal structure features into points on a 2D plane, enabling a more intuitive observation of the relationships between structures.

  下载: 全尺寸图片 幻灯片

  Table 1.  Comparison of results between the two prediction algorithms and the energy difference during structure relaxation (per atom).

  下载: 导出CSV

  Table 2.  Comparison of the BC₂P structure. Lattice constant a; bond lengths between B-C, C-C and C-P atoms; bond angles between B-C-B and C-P-C atoms; cohesive energy per atom.

  下载: 导出CSV
•