School of Science, Xi'an Jiaotong University, Xi'an 710049
在科研和生产实践中,有许多变量之间的关系都是非线性的。如果不借助计算机进行非线性拟合而用手工画图的方法,往往需要把数学模型经过变量代换转换成间接变量彼此之间的线性关系。这种转换往往有一定的局限性,而且手工画图随意性较大,最终得到的结果往往都存在较大的误差。随着电脑的普及和数据处理软件的应用,恢复变量之间的非线性直接表达形式,用非线性方法取代线性方法是数据处理的必然趋势。
在化学动力学部分,若一个反应的速率方程可以表示为rA=kAcAαcBβcCγ…,则仅当α、β、γ…以及kA完全确定以后,该速率方程才是确定的,才能将此方程具体用于分析和解决相关的化学动力学问题。可是,到底该如何确定反应级数α、β、γ…以及kA呢?
做实验时,如果反应物A的初始浓度远小于反应物B、C等的初始浓度,则反应过程中B、C等物质的浓度自始至终几乎不变。这时可将B、C等物质的浓度都近似当作常数。这时可以把反应速率方程改写为
|
$
{r_{\rm{A}}} = - \frac{{{\rm{d}}{c_{\rm{A}}}}}{{{\rm{d}}t}} = k'c_{\rm{A}}^\alpha
$
|
(1)
|
其中
|
$
k' = {k_{\rm{A}}}c_{{\rm{B,0}}}^\beta c_{{\rm{C,0}}}^\gamma \cdots
$
|
(2)
|
在一定温度下,k′近似为常数。这样处理,就如同把除A物质以外的其他物质对反应速率的影响都掩盖了,此时表面上反应速率只与A物质的浓度有关,故称此法为隔离法[1~9],也称为淹没法。在隔离法的基础上,可以测定多组(cA, t)数据,然后按照传统的建立反应速率方程的办法可分别用微分法或积分法(积分法亦称为尝试法)确定α;也可以在隔离法的基础上,测定多组(cA,0, t1/2,A)数据,然后用半衰期法确定α;同样用隔离法也可以把β、γ…分别确定下来。α、β、γ…都有了,再结合已有的实验数据,便可以把式(1)中的k′确定下来。有了k′之后,结合式(2)就可以把kA确定下来。这时,化学反应速率方程就完全确定了。
但使用这些传统的方法时,不仅工作效率低,而且积分法只适用于反应级数α、β、γ…为整数的情况;半衰期法需要在相同条件下进行多次实验,从而测定与多个不同初始浓度相对应的半衰期,结果会产生较大的误差;微分法虽原则上不论反应级数是几都适用,但使用微分法时,需要根据实验数据手工画曲线,在该曲线的不同点上作切线并求其斜率。此斜率就是该点上的反应速率。然后在式(1)的基础上,用反应速率的对数对浓度的对数作图可得一条直线,该直线的斜率便是反应级数α。使用微分法不仅费时费力,而且误差也大。
尽管传统的建立反应速率方程的方法存在种种弊端,但是目前许多与建立反应速率方程有关的物理化学教材中,普遍都只介绍这些传统方法,而不提及当今处理实验数据时高效且准确的非线性拟合法。这样处理不仅在教学过程中花费的时间较长,而且未能结合具体问题及时把学生应该学习和掌握的新方法传授给他们。
在个人电脑已经很普及的今天,非线性拟合法的使用范围越来越广泛,非线性拟合方法使用的效果非常好。余逸男[10]对乙酸乙酯皂化反应的实验数据用Matlab软件进行了非线性拟合。结果表明,用非线性拟合方法时的误差平方和约为传统手工方法的十五分之一。胡玮等[11]介绍了如何借助Origin软件把非线性拟合法用于沉降分析实验中的数据处理,从而得到的G~t曲线方程如下:
|
$
G = \left( {a + b/{t^Q}} \right) \cdot {{\text{e}}^{-c/t}}
$
|
|
其中,G是t时刻用扭力天平称得的质量,a、b、c和Q是用非线性拟合法得到的4个参数。欲用传统的手工方法得到这样的结果是不可思议的。赵玲等[12]研究了五氯酚(PCP)在二氧化锰作用下的降解反应动力学行为。他们采用n级反应速率模型、用Origin软件对PCP的降解动力学行为进行了非线性拟合,结果显示反应级数为n>0.999,这表明在二氧化锰作用下PCP的降解反应对于PCP是一级反应。与此同时,从这样的处理结果可以看出,使用非线性拟合方法时,对于一级反应和非一级反应可不必加以区分,均可采用n级反应速率模型进行处理。如果这样处理的结果表明反应为一级反应即n接近于1,这时可利用一级反应速率模型再次对实验数据进行处理,从而可得到更为准确的结果。对于粘度法测定高聚物分子量的一组实验数据(t, c),经过简单数据处理可得一组(ηsp/c, c)数据。周从山等[13]分别借助下面两个公式对这些实验数据做了非线性拟合和线性拟合
|
$
\begin{gathered}
t = {t_0} + {t_0}\left[\eta \right]c + m{t_0}{c^2} \\
{\eta _{{\text{sp}}}}/c = \left[\eta \right] + mc \\
\end{gathered}
$
|
|
从非线性拟合可得到特性粘度[η]和参数t0与m,从线性拟合可得到特性粘度[η]和参数m。借助Mark-Houwink经验公式,由特性粘度[η]即可得到待测高聚物的分子量。此处采用非线性拟合方法还有一个优点:纯溶剂流经粘度计毛细管的时间t0可通过非线性拟合得到,而不必专门测定。根据表面张力随浓度变化的实验测定结果(σ, c),也可以用非线性拟合法求得溶质分子的横截面积[14]。在与物理化学相关的数据处理问题上,还有许多非线性拟合法成功处理的范例。
总之,在计算机和相关数据处理软件的帮助下,非线性拟合法的使用范围非常广泛,而且数据处理结果的准确性会大幅度提高。在许多情况下,借助非线性拟合法还可以得到一些用传统的数据处理方法无法得到的参数,如粘度法测定高聚物分子量实验中纯溶剂流经毛细管的时间t0,又如表面张力测定实验中纯溶剂的表面张力σ0等。目前较常用的非线性拟合软件有Origin软件和Matlab软件。
在建立反应速率方程时,如果使用隔离法,使cA, 0远小于cB, 0、cC, 0…,此时反应速率可用式(1)表示。不论实际反应对A物质的级数α是几,对实验数据进行非线性拟合时α不会严格等于1。故不论α是多少,均可对式(1)作如下变形并积分
|
$
\int {-\frac{{{\text{d}}{c_A}}}{{c_A^a}} = \int {k'{\text{d}}t} }
$
|
|
所以 $\frac{{c_A^{1-a}}}{{\alpha-1}} = k't + C$ C为积分常数
即
|
$
t = \frac{1}{{\left( {\alpha-1} \right)k'}}c_{\text{A}}^{1-\alpha }-C/k'
$
|
|
或
|
$
t = Kc_{\rm{A}}^{1 - \alpha } + C'
$
|
(3)
|
其中
|
$
\begin{array}{l}
K = \frac{1}{{\left( {\alpha - 1} \right)k'}}\\
C' = - C/k'
\end{array}
$
|
(4)
|
式(3)中共有3个待拟合的参数即K、α和C′。在一定温度下,可借助多组实验数据(cA,t)对式(3)进行非线性拟合,从而得到参数K、α和C′。然后借助式(4)即可得到k′,进一步借助式(2)即可得到反应速率常数kA。运用此法同理可得到β、γ…,最终可得到一个确切的总反应速率方程。
例1 把一定量的纯氯甲酸三氯甲酯放入一个刚性密闭容器内。一定温度下氯甲酸三氯甲酯会发生反应ClCOOCCl3(g)2COCl2(g)。实验测得不同时刻容器内的总压力p见表 1。
表 1
Table 1
表 1(Table 1)
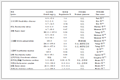
表 1 不同时刻氯甲酸三氯甲酯分解反应系统的总压力
Table 1 The total pressure of decomposition reaction of trichloromethyl chloroformate at different time
| t/s |
0 |
51 |
206 |
404 |
751 |
1132 |
1575 |
2215 |
| p/Pa |
2004 |
2064 |
2232 |
2476 |
2710 |
2969 |
3197 |
3452 |
|
表 1 不同时刻氯甲酸三氯甲酯分解反应系统的总压力
Table 1 The total pressure of decomposition reaction of trichloromethyl chloroformate at different time
|
求该反应的反应级数和实验温度下的速率常数。
解:ClCOOCCl3(g)2COCl2(g)
|
$
\begin{array}{*{20}{c}}
{t = 0}&{{P_{{\text{A}}, 0}}}&0 \\
{t = t}&{{P_{\text{A}}} = {P_{{\text{A}}, 0}}-x}&{2x}
\end{array}
$
|
|
总压为
|
$
P = {P_{{\text{A}}, 0}} + x
$
|
|
所以
|
$
\begin{array}{l}
x = p - {p_{{\rm{A}},0}}\\
\;\;{P_{\rm{A}}} = 2{p_{{\rm{A}},0}} - p
\end{array}
$
|
(5)
|
设该反应的反应级数为α,则
|
$
- \frac{{{\rm{d}}{p_{\rm{A}}}}}{{{\rm{d}}t}} = kp_{\rm{A}}^\alpha
$
|
(6)
|
对此式变形、积分并适当整理可得
|
$
t = Kp_A^{1-\alpha } + C
$
|
|
即
|
$
t = K{\left( {2{p_{{\rm{A}},0}} - p} \right)^{1 - \alpha }} + C
$
|
(7)
|
其中
|
$
K = \frac{1}{{\left( {\alpha - 1} \right)k}}
$
|
(8)
|
结合式(7)对表 1中的数据进行非线性拟合,可得待拟合参数的值如下:
|
$
\begin{array}{*{20}{c}}
{K = 40270}&{\alpha = 1.071}&{C =-23480}
\end{array}
$
|
|
由此可见该反应为一级反应,α原本应等于1。故令α=1,并对式(6)变形并积分可得
|
$
{P_{\text{A}}} = {P_{{\text{A}}, 0}}{{\text{e}}^{-kt}}
$
|
|
将此代入式(5)可得
|
$
P = 2{P_{{\rm{A}}, 0}}-{P_{{\rm{A}}, 0}}{{\rm{e}}^{-kt}}
$
|
(9)
|
结合式(9)再次对表 1中的数据进行非线性拟合,结果可得该反应的速率常数为
|
$
k = 5.84 \times {10^{-4}}{{\rm{s}}^{-1}}
$
|
|
原本根据第一次非线性拟合得到的K值,并借助式(8)便可以得到该反应的速率常数。但由于第一次非线性拟合得到的α与实际反应级数1存在明显差别,故利用第一次非线性拟合得到的K计算得来的反应速率常数必然也存在较大的误差。所以,在第一次非线性拟合的基础上,利用正确的反应级数并通过第二次非线性拟合才会得到更准确的反应速率常数。
例2 反应CH3CHO (g) CH4(g)+CO (g)是乙醛的气相热分解反应。把一定量乙醛放入518℃的刚性密闭容器内,在不同时刻测得容器内的总压力p见表 2。
表 2
Table 2
表 2(Table 2)

表 2 不同时刻乙醛分解反应系统的总压力
Table 2 The total pressure of decomposition reaction of acetic aldehyde at different time
| t/s |
0 |
73 |
242 |
480 |
840 |
1440 |
| p/kPa |
48.40 |
55.60 |
66.25 |
74.25 |
80.90 |
86.25 |
|
表 2 不同时刻乙醛分解反应系统的总压力
Table 2 The total pressure of decomposition reaction of acetic aldehyde at different time
|
求该反应的反应级数和518℃下的速率常数。
解:从反应物到产物,可以看出该反应类型与例1中的反应完全相同,故同样结合式(3)对表 2中的实验数据进行非线性拟合。拟合后可得
|
$
\begin{array}{*{20}{c}}
{K = 16740}&{\alpha = 1.92}&{C =-472}
\end{array}
$
|
|
由此可见:该反应为二级反应,α原本应等于2,故由式(7)可得
|
$
t = \frac{K}{{2{p_{{\rm{A}},0}} - p}} + C
$
|
(10)
|
结合式(10)再次对表 2中的实验数据进行非线性拟合可得
|
$
\begin{array}{*{20}{c}}
{K = 19450}&{C =-394.3}
\end{array}
$
|
|
将K值代入式(8)可得518℃下该反应的速率常数为
|
$
k = 5.14 \times {10^{-5}}{\rm{kP}}{{\rm{a}}^{-1}} \cdot {{\rm{s}}^{-1}}
$
|
|
根据前面的讨论,对于有一定级数的反应,不论反应级数是几,都可以用非线性拟合法来处理。即使对于一级反应也没有问题。因为实验测定结果都多少有点误差,对一级反应进行非线性拟合得到的反应级数α不会严格等于1,即|α-1|总会大于零。所以用非线性拟合法时,根本无需考虑反应是不是一级反应。
在隔离法的基础上,用非线性拟合法建立化学反应速率方程可分为两步。
第一步,结合式(3)初步对实验数据(t,c)进行非线性拟合,其中有K、α和C三个待拟合参数。如果一个反应有确定的级数,一般正确的反应级数都是整数或半整数。对于初步非线性拟合得到的结果,可观察分析得到的反应级数α与哪个整数或半整数接近,从而确定α的正确值。
第二步,从第一次非线性拟合看,如果不是一级反应即α≠1,就把正确的α值代入式(3),然后结合新得到的式(3)再次对实验数据进行非线性拟合。第二次进行非线性拟合时只有K和C两个待拟合参数。把第二次拟合得到的K值代入式(4),便可以得到常数k′。再结合式(2)便可以得到该反应的速率常数kA。
从第一次非线性拟合得到的结果看,如果是一级反应即α=1,则把α=1代入式(1),并变形积分可得
|
$
{c_{\rm{A}}} = {c_{{\rm{A,0}}}}{e^{ - k't}}
$
|
(11)
|
接下来,结合式(11)再次对实验数据进行非线性拟合。这时只有cA,0和k′这两个待拟合参数。从非线性拟合得到的k′,再结合式(2)便可以得到该一级反应的速率常数kA。与此同时,第二次非线性拟合还可以得到该反应中反应物A的初始浓度cA,0。
综上所述,对于有确定级数的反应,在建立反应速率方程方面,非线性拟合法可以完全取代所有的传统方法即微分法、积分法、半衰期法等。而且在使用非线性拟合方法时,不仅无需手工画图,省时省力,而且数据处理结果会比手工处理更准确。计算机还能自动根据数据处理结果绘出更精美更准确的图线。
由于利用计算机软件不论进行线性拟合还是非线性拟合,都是根据最小二乘法通过大量的计算来完成的。而且根据上述,非线性拟合法条理清楚,操作步骤也比较少。所以,在今后的有关化学动力学教材和教学方面,当涉及反应速率方程的建立问题时,可以考虑以非线性拟合法为主。对于传统的确定反应速率方程的方法可以不述及,或最多将其放在次要的位置,简单提一提就可以了。同时可以此为契机,为后续所有课程及实验的数据处理、为毕业设计等打下扎实的基础。
 2016,
Vol. 79
2016,
Vol. 79 Issue (6): 566-569
Issue (6): 566-569 2016,
Vol. 79
2016,
Vol. 79 Issue (6): 566-569
Issue (6): 566-569