Chongqing Liangping Vocational Education Center, Chongqing 405200, China
Abstract:
Based on the introduction of Arrhenius rate equation, this paper explained the concept of activation energy in the perspective of collision theory, transition state theory and Tolman statistics. The results showed that judging reaction rate by only activation energy was imprecise, and analyzed the question from the view of teaching and preparing test questions.
Key Words:
activation energy
threshold energy
potential energy barrier
collision theory
transition state theory
Tolman statistics
1 问题背景
近年各地高考化学卷中关于活化能考查的试题频现,审视后发现命题者对活化能的理解不到位,部分相关试题值得商榷。现以2012年高考浙江理综卷27题为例加以讨论。该题以甲烷自热重整制氢工艺为载体,将情境、内容与能力3者巧妙融合,着重考查学生对盖斯定律、反应速率、化学平衡及影响因素等中学化学核心知识点的掌握程度。其中第(2) 问,要求学生依据相关反应的活化能数据,判断初始阶段甲烷蒸气重整速率和甲烷氧化速率的大小关系。
有关活化能的概念,苏教版《化学反应原理(选修)》教材提出“活化分子的平均能量与所有分子的平均能量之差称为活化能”,而在过渡态理论介绍中又指出“过渡状态的平均能量与反应物分子的平均能量的差为反应的活化能”。这种“多样化”的表述无论是对中学生的学还是一线教师的教都会带来迷茫与理解障碍。因此,准确认识和理解活化能的概念将直接关系到学生对化学反应速率、机理的认识和研究。那么,究竟什么是活化能?是否反应的活化能越小,反应速率也就一定越快呢?拟在活化能概念诠释的基础上,进一步分析与探讨与活化能相关的一些教学问题。
2.1 阿仑尼乌斯活化能( Ea)
1889年,瑞典化学家阿仑尼乌斯(Arrhenius)在研究温度与蔗糖水解速率常数间的影响关系过程中,受范霍夫(Vant Hoff)相似研究的启示,在先求得速率常数 k 的自然对数ln k 的基础上,再和温度倒数1/T 作图后可获得一条直线(即Arrhenius图),由此归纳得到了反应速率常数与温度关系的经验公式:
|
$k\left( T \right)=A\cdot {{e}^{-\frac{{{E}_{a}}~}{RT}~}}$
|
(1)
|
|
$即{{E}_{a}}=R{{T}^{2}}~\frac{dlnk\left( T \right)~}{dT}$
|
(2)
|
式(1) (2) 中,A 为指前因子,与速率常数 k 有相同单位,温度 T 用绝对温标,R 是摩尔气体常数,Ea为活化能(也称阿仑尼乌斯活化能)。按照1996年国际纯粹与应用化学联合会(简称IUPAC)的观点[1],认为活化能 Ea的概念应定义为:Arrhenius图(ln k -1/ T )上的直(曲)线在温度 T 下的斜率即为反应的活化能。由于 Ea是通过实验测定出来的,因而也称为实验活化能。
在化学中一般将反应物只经一步生成产物的反应称为基元反应(或称为元反应),而通常见到的绝大多数化学反应实际上都是经多个基元反应复合的结果,即为总包反应(或称为复合反应)。对基元反应的 Ea,其物理意义是非常明确和清晰的;而若是总包反应,如已获知明确反应级数的总反应的速率方程,则总反应的活化能 Ea一般称为总反应的表观活化能,数值上就是所有基元反应相应活化能总的代数和。
2.2 活化能的多种诠释
阿仑尼乌斯认为,在反应体系中,并非全部反应物分子都可以发生化学反应并进一步生成产物分子的,只有其中很少数的、具有较高能值的分子(即活化分子)才可以实现转化,而对应的 Ea指的是1 mol活化分子与一般的普通分子相比所高出的能量值。可见,阿仑尼乌斯解释了为什么化学反应过程中需要活化能,但应如何准确地理解阿仑尼乌斯活化能?100多年来,科学家们基于各自不同的描述化学反应速率的理论视角,为理解活化能提供了多角度的诠释[2],如:
2.2.1 基于碰撞理论视角
在阿仑尼乌斯提出“活化状态”和“活化能”概念后,路易斯(Lewis)接受了这一观点并结合气体的分子运动理论,于1919年创立了碰撞理论。他首先将分子假想成是没有内部结构和内部运动自由度的坚硬球体,并把气相状态时双分子的反应(如A+B→P)看成是2个分子发生碰撞后的结果,继而通过理论计算分子的碰撞频率,总结出基元反应的反应速率常数表达式:
|
$k\left( T \right)=A\cdot {{T}^{\frac{1}{2}}}\cdot {{e}^{-\frac{{{E}_{c}}~}{RT}~}}$
|
(3)
|
式(3) 中,Ec表示的含义为A与B分子发生碰撞时1 mol发生反应的分子在对联心线上相对平动能应该具备的最小能量值,一般称为化学反应的“阈能”(或称为临界能)。若式(3) 与阿仑尼乌斯公式对比,可估算出反应活化能为:
|
${{E}_{a}}={{E}_{c}}+\frac{1}{2}RT$
|
|
依据碰撞理论的观点,只有当反应物分子在相互碰撞时的相对平动能高于一定的阈值时反应才会发生,因而化学反应需要活化能,而 Ec是化学反应存在活化能的本质原因。 Ec与温度无关,但对于不同的反应 Ec有不同的数值。
2.2.2 基于过渡态理论视角
1935年,基于统计热力学和量子力学视角,艾林(Eyring)、波兰尼(Polany)和埃文斯(Evans)等科学家提出了过渡态理论。该理论认为,在反应物分子生成产物分子过程中,会经历形成活化络合物的过渡状态,而要形成该过渡态必须具备一定的能量值,反应物分子与活化络合物状态间转化存在着平衡。如对于简单双分子反应:
|
$A+BC~\rightleftharpoons {{\left[ A\cdots B\cdots C \right]}^{\ne }}\to AB+C$
|
|
其中A代表单原子分子,BC代表双原子分子,A与BC接近并形成活化络合物[A…B…C]≠,此时B-C键还未彻底断裂,生成物AB中化学键也尚未完全生成,而后续的活化络合物逐渐分解变成产物的过程是慢过程,属于控速步骤,决定着整个总反应的反应速率。
由于反应物分子间相互作用的反应势能与其相对间距直接相关,在反应物转化为产物的过程中,体系的势能不断发生变化,据此可以得出反应过程中表征势能变化的势能面图,从而找到最佳的转化路线。若仍以A与BC的反应为例,可得到图 1的反应途径势能变化示意图[3],即反应物A和BC到生成物AB和C必须翻越相应势能垒 Eb(活化络合物势能与反应物势能之差),再考虑到实际反应温度与0 K 时零点活化能间的差距,计算时应选择修正后的量子能垒 E0。
过渡态理论最终推演后给出的反应速率常数与温度的关系式为:
|
$k\left( T \right)=A\cdot {{T}^{m}}\cdot {{e}^{-\frac{{{E}_{0}}~}{RT}~}}$
|
(4)
|
式(4) 中,m 包含了有关常数及与温度 T 有关的因子。若将式(4) 与阿仑尼乌斯公式对比,可估算出反应活化能为:
|
${{E}_{a}}={{E}_{0}}+mRT$
|
|
由上可见,苏教版《化学反应原理(选修)》教材基于过渡态理论给出的“过渡状态的平均能量与反应物分子的平均能量的差为反应的活化能”的观点并不准确。
2.2.3 基于托尔曼统计视角
托尔曼(Tolman R C)基于统计学的视角来处理单分子、双分子化学反应的反应速率与温度间关系,提出了基元反应活化能基于统计学角度的解释。即对单分子的基元反应A→P,假设反应物分子A共计有 N 个分子,在分子可能达到的量子态i上具备一定分布,存在统计平均值的意义,则特定温度时该反应的速率常数是各个量子态反应速率常数 ki的平均值,即:
|
$k\left( T \right)=\frac{\sum\limits_{i}{{{k}_{i}}{{e}^{-\frac{{{\varepsilon }_{i}}}{{{k}_{B}}T}~~}}}}{\sum\limits_{i}{{{e}^{-\frac{{{\varepsilon }_{i}}}{{{k}_{B}}T}~~}}}}$
|
(5)
|
式(5) 中,ε i表示i态分子能量,k B为玻尔兹曼常数。托尔曼进一步推导、整理给出的结果为:
|
${{E}_{a}}=\left\langle {{E}^{\ne }} \right\rangle -\left\langle E \right\rangle $
|
|
其中,<E ≠ >代表活化分子的平均摩尔能量,<E>则指反应物分子的平均摩尔能量。除单分子反应外,诸如双分子基元反应A+B→P经推导也可获得上述同样的结果。通常状况下,化学反应这一宏观体系,一般包含数量众多的分子,得到的各种物理量均为研究体系相应微观量的统计学上的平均值。因此,活化能 Ea基于托尔曼统计视角的解释反映的是活化能的统计性质,相较于上述其他反应速率理论,更确切地说明了 Ea的物理意义。因此,Ea的托尔曼统计诠释目前已被绝大部分学者所接受。
可见,碰撞理论中的阈能 Ec、过渡态理论中的势能垒 Eb(或修正后的量子能垒 E0) 与阿仑尼乌斯活化能 Ea并不完全一致,它们之间既有区别又有联系,具体见表 1。
表 1
Table 1
表 1(Table 1)
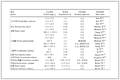
表 1 Ea、Eb(或E0) 与Ea的区别与联系[2]
Table 1 Differences and relations among Ec,Eb (or E0) and Ea
| 概念 | 活化能( Ea) | 阈能( Ec) | 势能垒( Eb) | 0 K活化能( E0) |
| 物理意义 | 1 mol活化分子的平均能量与1 mol反应物分子平均能量的差值 | 发生碰撞时1 mol反应分子在对联心线上相对平动能应该具备的最小的能量值 | 过渡态与反应物最低势能的差值 | 过渡态零点能与反应物零点能之间的差值 |
| 特征 | 统计量、宏观量 | 分子层面,微观量 | 分子层面,微观量 |
| 与 Ea关系 | - | Ea=Ec+ $\frac{1}{2}$ RT | Ea=E0+mRT |
| Ec、 E0与温度无关,在反应温度不太高时,与 Ea值非常接近 |
|
表 1 Ea、Eb(或E0) 与Ea的区别与联系[2]
Table 1 Differences and relations among Ec,Eb (or E0) and Ea
|
2.3 活化能与速率的关系
通过对阿仑尼乌斯速率方程式(1) 及其活化能的分析可知,指前因子 A 是一个只由“反应本性”决定而与反应温度、反应系统中各物质的浓度无关的常数,而 Ea在较小的温度段内可认为几乎保持不变。因此,在一定温度下,对于某一指定的化学反应,反应的速率常数 k 主要受活化能 Ea的影响;对于一定温度下不同的化学反应,由于反应所对应的 A 不一样,反应的速率常数 k 受反应各自 A 与活化能 Ea的综合影响。可见,2个不同的化学反应,仅凭相应活化能的大小来判断2者反应速率的快慢是不合适的,有时甚至是错误的。
常见的化学反应(比如甲烷、氢气等在氧气中的燃烧反应),并不是反应物分子间通过直接碰撞即可完成转化的,因此化学反应式多数情况下不能说明反应的发生过程,平时书写的这些化学反应都是总包反应。据查[4-5],原题介绍的甲烷的部分氧化和蒸气重整反应条件虽各不相同,但都需要在多相催化剂的参与下实现转化,是一个非常复杂的反应体系,包含了多步反应过程,涉及甲烷的部分氧化、燃烧、重整、水煤气变换、积炭等。所以,题中的化学反应是总包反应,对应的活化能是总反应的表观活化能。对于甲烷氧化和蒸气重整反应体系,各自的 A 值并不同,因而简单地仅以活化能大小作依据判断反应的反应速率大小,是武断的、不严密的。
此外,需要指明的是,对于给定的某化学反应,反应虽有确定的 A 值,但在特定催化剂催化或非催化条件下进行时却并不一样[6]。因此,催化剂之所以能加快反应速率的原因只归结于能够降低反应活化能的论述也是不准确的。
3 教学反思
通过以上探析,不仅对活化能概念等有了更深刻、全面的认识,结合自身的日常教学感悟也颇多。中学教材是基于对基元反应的碰撞理论与过渡态理论来阐释活化能的,是活化能知识学习的冰山一角,学生不可能对活化能概念有全面的认识。当然,受限于学生的认知水平,更不能引入阿仑尼乌斯速率方程、阈能、势能垒等内容。从命卷角度看,各地高考没有必要编制考查上述内容的考题来困扰考生,更不允许试题本身存在科学性硬伤。作为选拔考试用题,希望命题者能慎之又慎,充分重视高考命题的科学性和严谨性,否则不仅会增加学生学习负担,对学生后续深入学习科学概念也会产生负面影响。
 2016, Vol. 37
2016, Vol. 37  Issue(13): 64-66
Issue(13): 64-66  2016, Vol. 37
2016, Vol. 37  Issue(13): 64-66
Issue(13): 64-66